Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Dietlind Bäro
Daniel Metzsch | www.matheraum.de
Mathe für's ABI 2008
Aufgabenblatt 6
Abgabe: Mo 14.01.2008 08:00 | 17.12.2007 | | Aufgabe 1 | Dem menschlichen Körper können Medikamente durch einen Tropf kontinuierlich zugeführt
werden. Zu Beginn weist der Körper keine Medikamentenmenge auf, nach In-Gang-Setzen
des Tropfes erhöht sich die Medikamentenmenge mit jedem Tropfen, aber zugleich beginnen
Nieren und Leber die Substanz wieder auszuscheiden.
Die Funktion m: 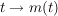 , t in Minuten, m in Milligramm gemessen, gebe die Medikamentenmenge , t in Minuten, m in Milligramm gemessen, gebe die Medikamentenmenge
im Körper an.
a. Erläutern Sie die Bedeutung der Ableitungsfunktion m für oben beschriebenen
Wachstumsprozess.
b. Für ein bestimmtes Medikament gelte 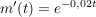 . .
Bestimmen Sie m(t) unter der Voraussetzung, dass der Tropf zur Zeit t = 0 gestartet wird.
Es gilt fortan: 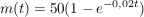 . .
c. Zeichnen Sie die Graphen von m und m für einen sinnvollen Zeitraum und interpretieren
Sie deren Verlauf bezüglich der Medikamentenzufuhr.
d. Erläutern Sie, dass 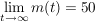 gilt. gilt.
Bestimmen Sie den Zeitpunkt, zu dem die Medikamentenmenge 90% dieses Grenzwertes
erreicht und den, von dem ab der Zuwachs des Medikaments weniger als 0,5 mg pro Minute beträgt.
e. Berechnen Sie 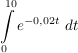 . Erläutern Sie die Bedeutung dieser Zahl. . Erläutern Sie die Bedeutung dieser Zahl.
f. Nach 5 Stunden wird der Tropf abgesetzt. Der Abbau des Medikaments erfolgt danach
mit einer Halbwertszeit von 6 Stunden.
Bestimmen Sie den Zeitpunkt, von dem ab die Nachweisgrenze des Medikaments von
1 μg 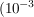 mg) im Körper unterschritten wird. mg) im Körper unterschritten wird.
|
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|