AustauschsatzAustauschsatz von Steinitz:
Sei  eine Basis und eine Basis und 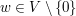 beliebig. beliebig.
Dann existiert mindestens ein  , sodass , sodass  Basis von Basis von 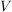 ist. ist.
Genauer gilt für  , dass man jeden Index , dass man jeden Index 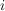 wählen kann, für den wählen kann, für den  ist. ist.
Erweiterung:
Seien  eine Basis und eine Basis und  linear unabhängig. linear unabhängig.
Dann existieren  , sodass , sodass  eine Basis von eine Basis von 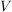 ist. Insbesondere gilt ist. Insbesondere gilt 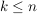 . .
Beweis zum Austauschsatz von Steinitz:
Beweisidee: Man zeige, dass unter den Voraussetzungen des Satzes von Steinitz  ein (1.) linear unabhängiges (2.) Erzeugendensystem ist. ein (1.) linear unabhängiges (2.) Erzeugendensystem ist.
Zum Beweis:
 ist Basis, ist Basis,  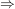  mit mit  nicht alle gleich nicht alle gleich 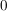 . .
Sei 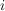 ein Index mit ein Index mit  . Man zeige nun, dass . Man zeige nun, dass  eine Basis ist. eine Basis ist.
(1.) linear unabhängig:
Zu zeigen:  mit mit  (*) (*) 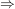 
Setze  in (*) ein: in (*) ein:

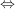  , ,
Aber  sind linear unabhängig. Daraus folgt sind linear unabhängig. Daraus folgt
 (-1-) und (-1-) und  (-2-) (-2-)  . .
Mit (-1-) folgt aus 
 , ,
woraus mit (-2-)
 
folgt, was zu zeigen war. 
(2.) Erzeugendensystem:
Zu zeigen: 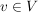 beliebig kann man schreiben als beliebig kann man schreiben als
 mit entsprechenden mit entsprechenden  . .
 erzeugen erzeugen 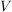 , d.h. , d.h.  : :
(a) 
(b)  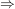 
Einsetzen von (b) in (a):
 
Beweis zur Erweiterung:
Beweisidee: Induktion nach k.
Zum Beweis: Vollständige Induktion
Induktionsanfang: 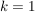
 ist eine Basis und ist eine Basis und  linear unabhängig. linear unabhängig. 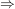  . Mit dem Austauschsatz von Steinitz folgt . Mit dem Austauschsatz von Steinitz folgt

Induktionsvoraussetzung (I.V.):
Der Satz gilt für alle  . .
Es gilt nun zu zeigen, dass aus der I.V. die Verifizierung des Satzes für  folgt. folgt.
Induktionsschritt: 
Seien  linear unabhängig. Aus linear unabhängig. Aus

folgt
 mit mit 
Behauptung: 
Beweis der Behauptung: Falls alle  , folgt , folgt


Das ist aber offensichtlich ein Widerspruch zur linearen Unabhängigkeit der  Also existiert ein Also existiert ein  mit mit  . .
Mit dem Austauschsatz von Steinitz folgt
 ist Basis. ist Basis. 
Beispiele:
(1.)  ist Basis des ist Basis des 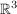 . Man weise dies zur Übung nach. . Man weise dies zur Übung nach.
Der Vektor  soll ausgetauscht werden. soll ausgetauscht werden.
1. Stelle 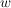 als Linearkombination der als Linearkombination der  dar. dar.

2. Identifikation austauschbarer Vektoren.
Nach dem Austauschsatz von Steinitz können wir den Vektor  austauschen, dessen Koeffizient austauschen, dessen Koeffizient  ist. Im vorliegenden Beispiel können wir also ist. Im vorliegenden Beispiel können wir also  oder oder  austauschen, nicht aber austauschen, nicht aber 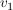 , da dessen Koeffizient gerade 0 ist. , da dessen Koeffizient gerade 0 ist.
3. Austausch unter Anwendung des Austauschsatzes.
Wir entscheiden uns  gegen gegen 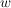 auszutauschen. Der Austauschsatz von Steinitz impliziert nun, dass auszutauschen. Der Austauschsatz von Steinitz impliziert nun, dass  ebenfalls eine Basis des ebenfalls eine Basis des 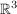 ist. ist.
(2.) Basisergänzung:
Ergänzung der Vektoren  und und  zu einer Basis zu einer Basis  von von  . .
1. Vorüberlegung:
Die Vektoren  müssen linear unabhängig sein, um zu einer Basis ergänzt werden zu können. Im vorliegenden Fall ist die einzige Lösung des linearen Gleichungssystems, das aus müssen linear unabhängig sein, um zu einer Basis ergänzt werden zu können. Im vorliegenden Fall ist die einzige Lösung des linearen Gleichungssystems, das aus

resultiert, wie man leicht sieht,  . (Man sieht so etwas "leicht", indem man die erste Zeile des linearen Gleichungssystems betrachtet, woraus . (Man sieht so etwas "leicht", indem man die erste Zeile des linearen Gleichungssystems betrachtet, woraus  folgt. Das impliziert wiederum folgt. Das impliziert wiederum  ) )
Also sind die beiden Vektoren linear unabhängig und mögliche Kandidaten für eine Basisergänzung.
2. Vorgehen:
Es ist evident, dass jede Basis des  aus 3 Vektoren besteht. Es bestehen zwei mögliche Vorgehensweisen aus 3 Vektoren besteht. Es bestehen zwei mögliche Vorgehensweisen  und und  zu einer Basis zu ergänzen. zu einer Basis zu ergänzen.
(1.) Der zu ergänzende Vektor  wird erraten. Man zeigt über die Definition einer Basis (nur lineare Unabhängigkeit zu prüfen), dass wird erraten. Man zeigt über die Definition einer Basis (nur lineare Unabhängigkeit zu prüfen), dass
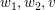
das gewünschte erfüllen, also tatsächlich eine Basis des  darstellen. darstellen.
(2.) Man nutzt den Austauschsatz und tauscht  gegen zwei Basisvektoren einer bekannten Basis des gegen zwei Basisvektoren einer bekannten Basis des  . Am naheliegendsten ist wohl die kanonische Basis des . Am naheliegendsten ist wohl die kanonische Basis des  , die, wie für jeden , die, wie für jeden 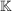 -Vektorraum -Vektorraum  , durch die Vektoren , durch die Vektoren
  
gegeben ist.
Während Möglichkeit (1.) die wohl zeiteffektivere ist, bietet Möglichkeit (2.) den Vorteil, dass sie bar jeder Kreativität ein eher algorithmisches bzw. standardisiertes Vorgehen aufweist und damit recht einfach handzuhaben ist. An dieser Stelle wird Möglichkeit (2.) weiter verfolgt.
3. Anwendung des Austauschsatzes von Steinitz:
Durch wiederholte Anwendung des Austauschsatzes von Steinitz, werden die Vektoren jeweils nacheinander ausgetauscht. Ebendieses Vorgehen wurde auch im Beweis der Erweiterung verfolgt. Das Verfahren gestaltet sich dabei wie folgt:
a)  wird als Linearkombination der wird als Linearkombination der  geschrieben. Es wird derjenige Vektor geschrieben. Es wird derjenige Vektor  ausgetauscht, dessen zugehöriger Koeffizient ausgetauscht, dessen zugehöriger Koeffizient  ist. ist.

Man hat nach dem Austauschsatz die Möglichkeit einen der Vektoren  gegen gegen  auszutauschen, um so eine Basis zu erhalten, da die Koeffizienten auszutauschen, um so eine Basis zu erhalten, da die Koeffizienten   sind. sind.
Nach Steinitz folgt, dass

eine Basis ist. Hierbei wird gemäß der Aussage des Satzes  gewählt, s.d. gewählt, s.d.  mit den Vektoren mit den Vektoren 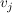 mit mit  eine Basis von eine Basis von  bildet. bildet.
b) Schritt a) wird für den Vektor  wiederholt. wiederholt.

Auch hier besteht die Möglichkeit alle drei Vektoren  auszutauschen, wobei die Wahl von auszutauschen, wobei die Wahl von  wohl nicht zielführend sein wird. Es wird daher wohl nicht zielführend sein wird. Es wird daher  gewählt, s.d. gewählt, s.d.  und und  zusammen mit allen zusammen mit allen 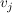 mit mit 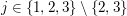 , also , also  , eine Basis bilden. , eine Basis bilden.
Also lassen sich  und und  durch den Vektor durch den Vektor 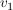 zu einer Basis zu einer Basis

ergänzen.
|