Benutzer:tobit09/StochastikL11Stochastisches Modellieren für Einsteiger
 4. Zufallsvariablen X 4. Zufallsvariablen X
Lösungsvorschlag zu Aufgabe 11
(i) 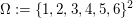
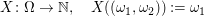
die Zufallsvariable "Augenzahl des ersten Würfels"
Das Ereignis "Zuerst eine 6 gewürfelt" lautet damit
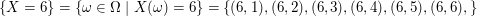 . .
(ii) 
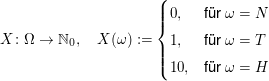
die Zufallsvariable, die für "Wert des Gewinns in Euro" steht
Das Ereignis "keine Niete" tritt genau dann ein, wenn der Wert des Gewinns 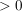 ist. Somit lässt es sich beschreiben durch ist. Somit lässt es sich beschreiben durch
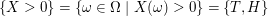 . .
|