Bernoulli-VersuchDer Ausgangspunkt ist wie folgt:
Es wird n Mal ein- und dasselbe Zufallsexperiment durchgeführt, bei dem lediglich von Interesse ist, ob ein bestimmtes Ereignis ("Erfolg") eingetreten ist oder nicht.
Die Wahrscheinlichkeit für das Eintreten dieses Ereignisses sei (jedes Mal) p, und man nimmt an, dass die Ausgänge der einzelnen Experimente sich gegenseitig nicht beeinflussen.
Beschreibt die Zufallsvariable X die Anzahl der Erfolge unter diesen n zufälligen Versuchen, so ist X binomialverteilt mit Parametern n und p.
Beispiele:
- Anzahl des Ereignisses "Kopf" beim zwanzigfachen Wurf einer fairen Münze (
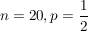 ) )
- Anzahl des Ereignisses "Augenzahl 5 " beim zehnmaligen Wurf eines fairen Würfels (
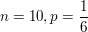 ) )
Die Formel für die Wahrscheinlichkeit, dass X einen bestimmten Wert k annimmt (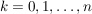 ), lautet ), lautet
- Wahrscheinlichkeit Münzwurf, 7 "Kopf":
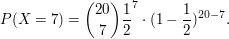
- Wahrscheinlichkeit Würfel, 3 mal "5":
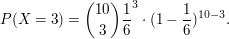
Diese Formel ergibt sich aus den obigen Annahmen so:
Ist die beobachtete Anzahl der Erfolge gleich k, so ist das interessierende Ereignis genau k Mal und demnach das Gegenereignis genau n-k Mal eingetreten.
Da die Ereignisse der einzelnen Experimente stochastisch unabhängig auftreten (keine gegenseitige Beeinflussung), wird insgesamt k Mal die Wahrscheinlichkeit p und n-k Mal die Wahrscheinlichkeit 1-p multipliziert. So erklärt sich der Ausdruck
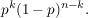
Dieses Ergebnis erhält man bei Betrachtung einer ganz bestimmten Folge von Erfolgen und Misserfolgen (z.B. die ersten k Versuche Erfolg und anschließend n-k Mal Misserfolg). Da es aber unwichtig ist, wann die k Erfolge eintreten (es ist nur wichtig, dass sie eintreten), muss man noch die Anzahl der Möglichkeiten berücksichtigen, die k Erfolge unter den n Versuchen zu platzieren. Dafür gibt es gerade 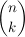 Möglichkeiten (Binomialkoeffizient). Da das Ereignis Möglichkeiten (Binomialkoeffizient). Da das Ereignis 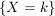 gerade die Vereinigung aller möglichen Folgen mit k Erfolgen darstellt, addiert man die Wahrscheinlichkeit gerade die Vereinigung aller möglichen Folgen mit k Erfolgen darstellt, addiert man die Wahrscheinlichkeit 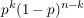 insgesamt insgesamt 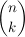 Mal, woraus sich die oben stehende Formel ergibt. Mal, woraus sich die oben stehende Formel ergibt.
Der Binomialkoeffizient
gibt die Anzahl von Möglichkeiten an, aus einer Menge von n Elementen genau k Elemente ohne Wiederholung und ohne Berücksichtigung der Reihenfolge zu entnehmen. Die Formel erklärt sich wie folgt. Beim k-maligen Ziehen ohne Wiederholung gibt es
verschiedene Möglichkeiten. Da die Reihenfolge der gezogenen Elemente keine Rolle spielt, muss man durch die Anzahl der Permutationen in dieser Menge von k Elementen dividieren, also durch k! teilen, woraus die angegebene Formel folgt.
|