DefinitionsbereichDefinitionsbereich einer Funktion
... heißt die Menge derjenigen reellen Zahlen, für die eine Funktion definiert ist.
Man ermittelt den Definitionsbereich, indem man die Zahlen sucht, für die die Funktion nicht definiert ist; z. B. weil der Nenner einer gebrochen rationalen Funktion Null würde. Die Zahlen schließt man aus der Menge der reellen Zahlen aus:
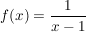
Setzt man hier 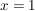 ein, so wird der Nenner Null und der Bruch ist nicht definiert. ein, so wird der Nenner Null und der Bruch ist nicht definiert.
Der Definitionsbereich 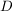 ist daher: ist daher: 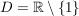
Bemerkungen.
Obige Definition ist speziell für die Schule sehr geeignet. Eine allgemeine Definition findet man etwa unter dem Begriff Zielbereich.
|