Funktionsgrenzwertbestimmung
Das Ziel ist immer das Gleiche:
Schreibe den Funktionsterm derart, dass du es "sehen" kannst, was für 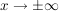 passiert. passiert.
Der Weg dahin hängt aber von der Art des Funktionsterms ab.
Beispiel: ganzrationale Funktionen (was ich hier jetzt aufschreibe, überlegt man sich nur einmal, danach "weiß" man es)
Das kannst du etwa so schreiben:
Da die Klammer gegen 1 konvergiert (setze probeweise "große Zahlen" wie 10, 100,.. ein), bestimmt also einzig und allein der Summand mit dem höchsten Exponenten (im Originalterm) über das Verhalten gegen 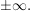
So kommst du ganz leicht zu einem Kriterium für ganzrationale Funktionen:
- Unterscheidung zwischen geradem und ungeradem Grad (bei
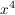 geht es beide Male in die gleiche Richtung, bei geht es beide Male in die gleiche Richtung, bei 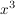 einmal so und einmal so) einmal so und einmal so)
- Unterscheidung zwischen dem Vorzeichen vor diesem Summand
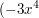 führt ja dazu, dass das in beide Richtungen gegen führt ja dazu, dass das in beide Richtungen gegen 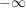 abhaut) abhaut)
Bei gebrochen-rationalen Funktionen macht man das ähnlich (vielleicht kommt dir das von den Folgen bekannt vor):
Beispiel:
Du klammerst die höchste überhaupt auftretende Potenz von x im Nenner und im Zähler aus und kürzt:
Dann siehst du, was passiert: Zähler geht gegen 0, Nenner gegen 1 und fertig.
Daraus kannst du dir dann auch ein einfaches Kriterium für gebrochen-rationale Funktionen machen, wenn du es einmal durchgerechnet hast:
- Ist der Exponent oben größer, haut es gegen
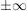 ab (hängt dann wie bei den ganzrationalen vom Vorzeichen ab). ab (hängt dann wie bei den ganzrationalen vom Vorzeichen ab).
- Ist der Exponent unten größer (wie im Beispiel), geht es gegen 0.
- Ist der max. Exponent oben und unten gleich, geht es gegen eine feste Zahl, nämlich gerade den Quotienten der Koeffizienten davon.
Steht etwa sowas da:
dann geht das
Tauchen Exponentialfunktionen auf, gibt es kein so ganz einheitliches Vorgehen mehr, da braucht man in der Regel nur folgendes Wissen:
Beispiel: sei 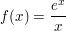 : :
- Die Exponentialfunktion wächst bzw. fällt für
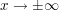 stärker als jede Potenz von x, ist also Grenzwert bestimmend. stärker als jede Potenz von x, ist also Grenzwert bestimmend.
Die Exponentialfunktion geht für 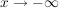 schneller gegen 0 als schneller gegen 0 als 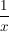 gegen gegen 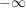 geht. geht.
Ähnliches gilt natürlich für Logarithmen.
Wurzeln sind ja im wesentlichen auch nur Potenzen von x 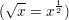 kannst du also auch ähnlich argumentieren. kannst du also auch ähnlich argumentieren.
Sinus und Cosinus sind immer beschränkt, das Verhalten des Tangens ist auch klar.
Bei Kombinationen von denen hilft es dir eigentlich am meisten, immer nach dem Verhalten der Einzelnen zu schauen und dann Grundwissen zu benutzen.
Beispiel:
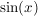 bleibt immer zwischen -1 und 1, spielt also für die Grenzwerte keine Rolle. Entscheidend ist also das Verhalten von bleibt immer zwischen -1 und 1, spielt also für die Grenzwerte keine Rolle. Entscheidend ist also das Verhalten von 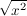 und das ist dir bekannt. und das ist dir bekannt.
|