GrenzwertbestimmungWie berechne ich den Grenzwert einer Folge?
Nun ja, das kommt darauf an, in welcher Form Du die Folge gegeben hast.
Manchmal ist es gar nicht so einfach, den Grenztwert einer Folge zu bestimmen, aber mit ein paar Rechenregeln und Tricks kommt man doch schon recht weit, deshalb hier vielleicht mal ein paar Beispiele:
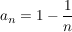
Für große n wird 1/n seeeehr sehr klein, deswegen geht die Folge gegen 1.
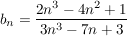
hier hilft uns vielleicht ein kleiner Rechentrick, auch wenns zunächst komplizierter aussieht: wir klammern n³ aus:
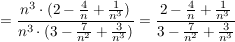 . .
Wie man sieht (oder sich mit einem Taschenrechner leicht verdeutlichen kann), gehen alle die "Schrotterme", wo im Nenner n^ hoch irgendwas steht, gegen Null, so daß am Ende nur noch 2/3 stehenbleibt, also ist der Grenzwert hier 2/3.
Nun vielleicht ein etwas komplexeres Beispiel:
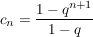 für 0<q<1. für 0<q<1.
Dazu sehen wir uns erstmal an, was der Term 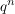 für große n macht. Allgemein ist, da q zwischen 0 und 1 liegt für große n macht. Allgemein ist, da q zwischen 0 und 1 liegt 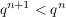 , also werden die Folgenglieder immer kleiner für wachsendes n und werden sogar beliebig viel kleiner. , also werden die Folgenglieder immer kleiner für wachsendes n und werden sogar beliebig viel kleiner.
Andererseits aber sind die Folgenglieder aber für jedes n auch größer als 0, so daß 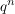 gegen null geht für n gegen unendlich. gegen null geht für n gegen unendlich.
(die Argumentation war natürlich jetzt nicht mathematisch korrekt aufgeschrieben, aber ich wollte einfach anschaulich machen, worum es geht...)
Nun zu dem größeren Term.
Da ist jetzt klar, daß der, da 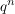 gegen 0 geht, gegen gegen 0 geht, gegen 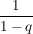 geht. geht.
Was sind Infimum und Supremum?
Fangen wir erstmal damit an: dir dürfte bekannt sein, was eine obere bzw. untere Schranke ist. Zum Beispiel hat die Menge M={1,2,7,3,9} zum Beispiel die 10 als obere Schranke, da kein Element der Menge M größer ist als 10. Wie man sieht, ist die obere Schranke nicht eindeutig, denn auch 12348.5 wäre eine obere Schranke.
Das supremum ist nun definiert als kleinste obere Schranke. Wie man sich leicht überlegen kann, ist das supremum eindeutig bestimmt, im obigen Falle wäre z.B. sup M = 9.
Das supremum muß nicht unbedingt Element der Menge sein, nehmen wir z.B. N=[0,1), also das rechts offene Intervall von 0 bis 1.
Offensichtlich ist sup N =1, denn zu allem, was kleiner 1 ist, gibt es ja immer noch ein Element, das größer ist und trotzdem kleiner 1.
Dennoch ist 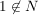 . .
Analog dazu ist das infimum die größte untere Schranke.
|