Gruppe von PermutationenDefinition Gruppe von Permutationen
Universität
Ursprünglich fasste man Gruppentheorie auf als das Studium von nichtleeren Teilmengen 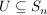 (siehe symmetrische Gruppe, für die mit je 2 Elementen (siehe symmetrische Gruppe, für die mit je 2 Elementen 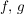 aus aus 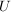 auch auch 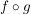 aus aus 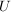 ist. Da das Assoziativgesetz und die Kürzungsregeln gelten (sie gelten bereits in ist. Da das Assoziativgesetz und die Kürzungsregeln gelten (sie gelten bereits in 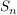 ) handelt es sich bei diesen Mengen auch um Gruppen, sogenannte Gruppen von Permutationen (vom Grad ) handelt es sich bei diesen Mengen auch um Gruppen, sogenannte Gruppen von Permutationen (vom Grad  ). ).
Erst die abstrakte Axiomatisierung durch Cayley verhalf der Gruppentheorie zum entscheidenen Durchbruch. Dass aber durch die abstrakte Formulierung "eigentlich" nichts Neues gefunden wurde, word nun mittels des Isomorphiebegriffes geklärt:
Es sei  eine Gruppe. Für jedes eine Gruppe. Für jedes 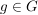 definiert man definiert man 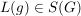 durch durch
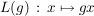 . .
Das Assoziativgesetz, 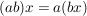 für alle für alle 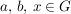 , ist äquivalent zu , ist äquivalent zu
(*) 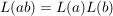 für alle für alle 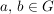 . .
Sei 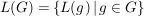 . (*) zeigt, dass . (*) zeigt, dass 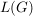 eine Halbgruppe ist (eine Unterhalbgruppe von eine Halbgruppe ist (eine Unterhalbgruppe von 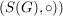 . Ferner ist . Ferner ist 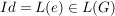 und jede Permutation und jede Permutation 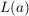 hat ein Inverses in hat ein Inverses in 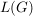 , nämlich , nämlich 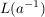 . Damit ist . Damit ist 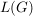 eine Gruppe von Permutationen. eine Gruppe von Permutationen.
Betrachten wir nun die Abbildung
![$ L\, : \, \begin{array}{ccc} G & \to & L(G) \\[5pt] g & \mapsto & L(g) \end{array} $ $ L\, : \, \begin{array}{ccc} G & \to & L(G) \\[5pt] g & \mapsto & L(g) \end{array} $](/teximg/9/1/00392119.png) , ,
so zeigt (*) auch, dass dies ein Homomorphismus ist.
Sei 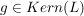 , , 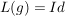 . Wenden wir beide Seiten dieser Gleichung auf das neutrale Element . Wenden wir beide Seiten dieser Gleichung auf das neutrale Element  an, so folgt an, so folgt 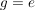 . Also ist . Also ist 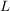 auch injektiv. auch injektiv. 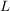 ist damit ein Isomorphismus von ist damit ein Isomorphismus von  auf auf 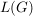 . Wir haben bewiesen: . Wir haben bewiesen:
Satz (Cayley): Jede Gruppe G ist isomorph zu einer Gruppe von Permutationen von G.
Insbesondere ist jede Gruppe der Ordnung  isomorph zu einer Gruppe von Permutationen vom Grad isomorph zu einer Gruppe von Permutationen vom Grad  . .
Quelle: isbn3446130799
|