Herleitung-eWie kommt man auf die Definition der Euler'schen Zahl:
Man hat sich das so gedacht: Man suchte eine Exponentialfunktion, die bei x=0 den Anstieg 1 haben sollte.
Oder in anderen Worten: Man suchte eine Funktion, die die Gerade y=x+1 in A(0|1) berühren sollte.
Ihre Form sollte einfach nur 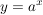 sein. sein.
Wenn man ein paar Exponentialfunktion testet, bekommt man mit, dass diese gesuchte Basis der Potenz zwischen 2 und 3 liegen muss.
Dann hat man sich dem Punkt langsam genähert und dabei alle Funktionsgleichungen der Exponentialfunktion aufgestellt.
Ich fange mal an:
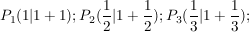 ... ... 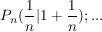
Wie man sieht, nähern sich die Punkte dem Punkt A(0|1) auf der Gerade y=x+1.
Und nun berechnet man die Basis a der Exponentialgleichung, die durch die Punkte 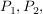 ... ... 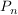 gehen: gehen:
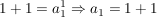 (=2) (=2)
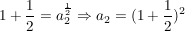 (=2,25) (=2,25)
...
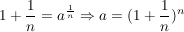
Und dieser Grenzwert ist zufälligerweise die Eulersche Zahl e,
nein, im Ernst, diese Zahl wurde bereits vom großen Mathematiker Leonhard Euler so benannt.
|