KrümmungBei Kurven in der Ebene kann man von der Krümmung sprechen:
Gerade: Linie ohne Krümmung
Kreis: Kurve mit konstanter Krümmung
Je kleiner der Radius des Kreises, umso stärker ist er gekrümmt.
So kommt man zur
Definition:
Die Krümmung eines Kreises ist der reziproke Wert seines Halbmessers: 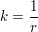
Die Krümmung einer Geraden ist gleich null: k=0
Allgemeinere Kurven:
Bei anderen Kurven kann die Krümmung von Punkt zu Punkt variieren. Um trotzdem zu einem (lokalen) Krümmungsbegriff zu kommen, nähert man die Kurve in der Umgebung eines Kurvenpunktes P auf die beste mögliche Weise durch einen Kreis, den "Schmiegekreis" oder "Krümmungskreis" an. Dessen Radius r ist der Krümmungsradius der Kurve im Punkt P , und dessen Kehrwert
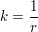
ist die Krümmung der Kurve im Punkt P (bzw. deren Betrag; siehe "Vorzeichen der Krümmung"). Der Mittelpunkt des Krümmungskreises ist "Krümmungsmittelpunkt". Er liegt auf der im Kurvenpunkt P errichteten Kurvennormalen.
Zur Berechnung der Krümmung benützt man die Differentialrechnung. Ist die Kurve durch eine Funktionsgleichung y=f(x) gegeben, so berechnet sich die Krümmung nach der Formel
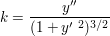
Aus der Formel ist auch ersichtlich, welche Voraussetzungen erfüllt sein müssen, damit die Krümmung definiert ist: f muss zweimal differenzierbar sein.
Vorzeichen der Krümmung:
Diese Formel liefert je nach dem Vorzeichen von 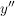 auch ein Vorzeichen für die Krümmung. Dabei bedeutet ein positives Vorzeichen, dass der Krümmungsmittelpunkt oberhalb des Kurvenpunktes P liegt und die Kurve im Punkt P linksgekrümmt ist. Negatives Vorzeichen entspricht einer Rechtskrümmung. auch ein Vorzeichen für die Krümmung. Dabei bedeutet ein positives Vorzeichen, dass der Krümmungsmittelpunkt oberhalb des Kurvenpunktes P liegt und die Kurve im Punkt P linksgekrümmt ist. Negatives Vorzeichen entspricht einer Rechtskrümmung.
Krümmung bei Flächen:
Der Krümmungsbegriff kann auch auf Flächen und höherdimensionale Gebilde erweitert werden. So ist z.B. die Kugelfläche eine Fläche konstanter Krümmung im Raum 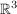 . .
Weiteres siehe bei Wikipedia: Krümmung
|