LHospitalscheRegelSatz L'Hospitalsche Regeln
1. Regel (Typ " ") ")
Die Funktionen 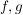 seien stetig auf seien stetig auf ![$ [a,b] $ $ [a,b] $](/teximg/9/5/00000959.png) und differenzierbar auf und differenzierbar auf ![$ ]a,b[ $ $ ]a,b[ $](/teximg/9/7/00043379.png) . .
Es sei 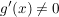 für alle für alle ![$ x\in]a,b[ $ $ x\in]a,b[ $](/teximg/8/1/00080818.png) , ,
Gilt nun 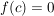 und und 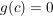 mit mit ![$ c\in]a,b[ $ $ c\in]a,b[ $](/teximg/1/2/00080821.png) und existiert und existiert 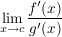 (einseitig bzw. beidseitig), dann ist (einseitig bzw. beidseitig), dann ist
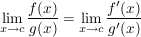 . .
Diese Regel gilt übrigens auch für 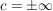 (und entsprechender Vergrößerung des Intervals (und entsprechender Vergrößerung des Intervals ![$ ]a,b[ $ $ ]a,b[ $](/teximg/9/7/00043379.png) zu zu ![$ ]-\infty,b[ $ $ ]-\infty,b[ $](/teximg/5/2/00080825.png) bzw. bzw. ![$ ]-\infty,\infty[ $ $ ]-\infty,\infty[ $](/teximg/6/2/00080826.png) bzw. bzw. ![$ ]-\infty,\infty[=\IR $ $ ]-\infty,\infty[=\IR $](/teximg/7/2/00080827.png) ) )
2. Regel (Typ "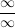 ") ")
Die Funktionen 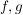 seien differenzierbar auf seien differenzierbar auf ![$ ]a,b[ $ $ ]a,b[ $](/teximg/9/7/00043379.png) . .
Es sei 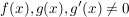 für alle für alle ![$ x\in]a,b[ $ $ x\in]a,b[ $](/teximg/8/1/00080818.png) . .
Gilt nun 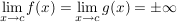 mit mit ![$ c\in]a,b[ $ $ c\in]a,b[ $](/teximg/1/2/00080821.png) und existiert und existiert 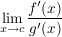 (einseitig bzw. beidseitig), dann ist (einseitig bzw. beidseitig), dann ist
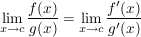 . .
Diese Regel gilt übrigens auch für 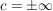 (und entsprechender Vergrößerung des Intervals (und entsprechender Vergrößerung des Intervals ![$ ]a,b[ $ $ ]a,b[ $](/teximg/9/7/00043379.png) zu zu ![$ ]-\infty,b[ $ $ ]-\infty,b[ $](/teximg/5/2/00080825.png) bzw. bzw. ![$ ]-\infty,\infty[ $ $ ]-\infty,\infty[ $](/teximg/6/2/00080826.png) bzw. bzw. ![$ ]-\infty,\infty[=\IR $ $ ]-\infty,\infty[=\IR $](/teximg/7/2/00080827.png) ) )
Zusammenfassung
1.
a) 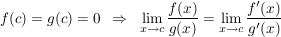 (Regel 1) (Regel 1)
b) 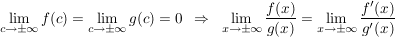 (Regel 1) (Regel 1)
2.
a)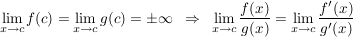 (Regel 2) (Regel 2)
b)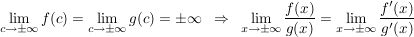 (Regel 2) (Regel 2)
Bemerkungen.
Die Regel beruht darauf, dass sich Funktionen in der Nähe" einer Stelle 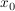 durch ihre Tangenten annähern lassen. durch ihre Tangenten annähern lassen.
Ist (im Standardfall") 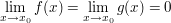 , so lauten die Tangentengleichungen , so lauten die Tangentengleichungen 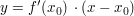 und und 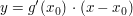 . Ihr Quotient . Ihr Quotient 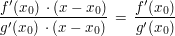 ist also eine Näherung für ist also eine Näherung für 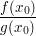 . .
Beispiele.
1.
Es sei 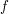 stetig differenzierbar in einer Umgebung von stetig differenzierbar in einer Umgebung von 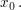 Dann liefert die Anwendung von der Regel von de l'Hôpital bei Dann liefert die Anwendung von der Regel von de l'Hôpital bei 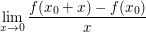 nichts anderes als nichts anderes als 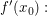
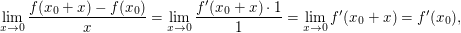
wobei die letzte Gleichheit wegen der Stetigkeit(!) von 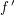 (!!) in (!!) in 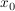 gilt. gilt.
Dieses Beispiel wirkt zwar trivial, aber es wird deswegen aufgeführt, weil die Regel von de l'Hôpital oft auch angewendet wird, obwohl man auch ohne sie auskäme. (Der Sinn dieses Beispiels liegt also tatsächlich darin, sich klarzumachen, ob ein gesuchter Grenzwert sich vielleicht nicht auf anderem Wege - hier: mithilfe der Definition der Ableitung an einer Stelle - direkt ergibt).
Wir führen ein Standardbeispiel auf, wo man sogar ohne de l'Hôpital den gesuchten Grenzwert direkt per Definitionem der Ableitung berechnen kann. In der Literatur gängig aufgeführt wird die Berechnung von
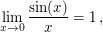
welche mit de l'Hôpital und der Stetigkeit von 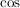 in in 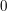 aus aus
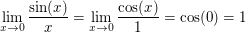
folgt. Dabei kann man dies mit 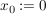 direkt aus direkt aus
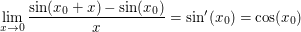
erkennen - wegen 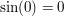 ist nämlich ist nämlich

Bemerkung:
Man beachte, dass die Differenzierbarkeit von 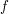 in in 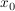 auch die Stetigkeit von auch die Stetigkeit von 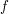 in in 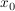 zur Folge hat, so dass zur Folge hat, so dass 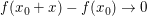 bei bei 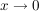 gilt. gilt.
2.
Wenn man *nur* weiß, dass 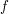 stetig in stetig in 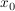 ist, dass ist, dass 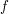 differenzierbar in einer Umgebung von differenzierbar in einer Umgebung von 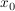 ohne ohne 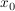 ist und zudem sei die Differenzierbarkeitsfrage in ist und zudem sei die Differenzierbarkeitsfrage in 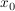 selbst nicht geklärt, so gilt: selbst nicht geklärt, so gilt:
Falls
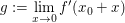
existiert, so existiert auch 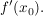 Denn: Sei Denn: Sei 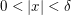 mit einem hinreichend kleinen mit einem hinreichend kleinen 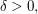 so folgt wie oben so folgt wie oben
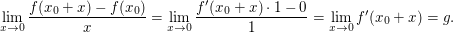
Wegen
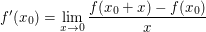 (wenn der Grenzwert rechterhand existent ist) (wenn der Grenzwert rechterhand existent ist)
folgt dann
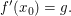
Bemerkung:
Insbesondere ist dann also auch 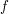 stetig differenzierbar in stetig differenzierbar in 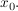
Beweis.
siehe: ![Link auf "http://de.wikibooks.org/wiki/Beweisarchiv:_Analysis:_Differentialrechnung:_L%27Hospitalsche_Regel" [link]](/images/popup.gif) WikiBooks WikiBooks
|