MatrixInvertierungGaussJordanGegeben sei eine invertierbare Matrix 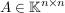 ( (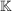 beliebiger Körper, z.B. beliebiger Körper, z.B. 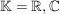 ). ).
Gesucht ist eine Matrix 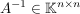 mit mit 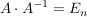 ( (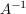 heißt dann die inverse Matrix zu A). heißt dann die inverse Matrix zu A).
Ermittlung von 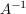 mittels Gauß-Jordan-Verfahren. Man darf auch hier nach den Regeln der elementaren Umformung vorgehen, allerdings empfiehlt sich kein Tauschen von Zeilen oder Spalten. Tauscht man eine Zeile, so ändert sich auch die Einheitsmatrix, sie muß am Ende in der getauschten Form auf der linken Seite stehen. Beim Tauschen von Spalten muß dies auf der rechten und auf der linken Seite geschehen, tauscht man links Spalte mittels Gauß-Jordan-Verfahren. Man darf auch hier nach den Regeln der elementaren Umformung vorgehen, allerdings empfiehlt sich kein Tauschen von Zeilen oder Spalten. Tauscht man eine Zeile, so ändert sich auch die Einheitsmatrix, sie muß am Ende in der getauschten Form auf der linken Seite stehen. Beim Tauschen von Spalten muß dies auf der rechten und auf der linken Seite geschehen, tauscht man links Spalte 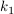 mit mit 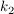 , so muss man dies auch auf der rechten Seite tun. , so muss man dies auch auf der rechten Seite tun.
Schreibe die Koeffizienten der Matrix A und die der Einheitsmatrix 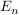 nebeneinander: nebeneinander:
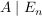
Nun bringe durch Zeilenumformungen (Multiplikation einer Zeile mit einem Körperelement, Addition zweier Zeilen) die linke Seite auf obere Dreiecksgestalt (rechts in der Einheitsmatrix alle Schritte analog durchführen). Danach elemeniere auch alle Elemente oberhalb der Diagonalen durch Zeilenumformungen.
(Sollte ein Diagonalelement 0 sein, ist die Matrix nicht invertierbar.)
Zum Schluß noch jede Zeile so multiplizieren, dass links die Einheitsmatrix steht.
Hat man auf der linken Seite die Einheitsmatrix erreicht, so befindet sich auf der rechten Seite die inverse Matrix zur A:
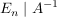
Die Umformungen auf der linken Seite sind gerade die des Gauß-Jordan-Verfahrens.
Vor Klausuren sollte man einige Beispiele rechnen, damit man dies sehr schnell kann und dadurch keine Zeitverluste in Kauf nehmen muss.
Beispiel:
Invertiert werden soll die Matrix
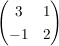
Schreibe Einheitsmatrix daneben:
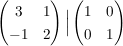
untere Zeile plus  der oberen Zeile: der oberen Zeile:
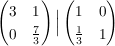
untere Zeile mit  multiplizieren: multiplizieren:
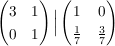
obere Zeile minus unterer Zeile:
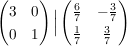
obere Zeile durch 3 teilen:
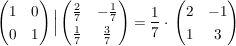
nun steht links die Einheitsmatrix und damit rechts die Inverse.
Probe mit 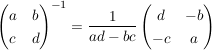 liefert das selbe Ergebnis. liefert das selbe Ergebnis.
|