NebenklasseDefinition
Sei  eine Gruppe, eine Gruppe, 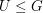 eine Untergruppe von eine Untergruppe von  und und 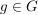 . Dann heißt . Dann heißt
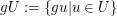 Linksnebenklasse von Linksnebenklasse von 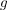 nach nach 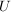 und und
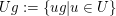 Rechtsnebenklasse von Rechtsnebenklasse von 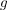 nach nach 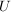 . .
Satz
Sei 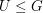 eine Untergruppe der Gruppe eine Untergruppe der Gruppe  . Dann gilt: . Dann gilt:
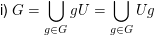
ii) Für je zwei Elemente 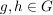 gilt gilt 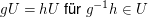 und und 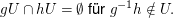 (Analoges gilt für die Rechtsnebenklassen.) (Analoges gilt für die Rechtsnebenklassen.)
iii) 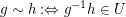 definiert eine Äquivalenzrelation auf definiert eine Äquivalenzrelation auf  , deren Äquivalenzklassen gerade die Links-/Rechtsnebenklassen sind. , deren Äquivalenzklassen gerade die Links-/Rechtsnebenklassen sind.
Beweis
Die Aussagen sind evident und damit eine gute Übung für den Anfänger der Algebra.
Bemerkung
Der Begriff der Nebenklasse wird insbesondere zur Definition des Faktor- bzw. Quotientenraums genutzt.
Literatur
isbn9783827430113 C. Karpfinger, K. Meyberg: Algebra, Springer Spektrum, 2013
|