PythagorasSatz des Pythagoras
Voraussetzungen und Behauptung
In jedem rechtwinkligen Dreieck gilt:
Die Summe der Quadrate über den Katheten ist gleich dem Quadrat über der Hypotenuse.
Bemerkungen.
(1) Sind  , , 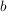 und und  die Seiten des rechtwinkligen Dreiecks und liegt der rechte Winkel der Seite die Seiten des rechtwinkligen Dreiecks und liegt der rechte Winkel der Seite  gegenüber, so gilt: gegenüber, so gilt:
(2) Auch im Dreidimensionalen gilt die Erweiterung dieses Satzes durch doppelte Anwendung:
Die Raumdiagonale in einem Quader mit den Kantenlängen a, b und c hat die Länge:
Beweis nach Garfield
{picture file=img/wiki_up//Satz des Pythagoras.jpg}
In das Quadrat 1 mit der Seitenlänge 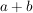 ist ein Quadrat 2 mit der Seitenlänge ist ein Quadrat 2 mit der Seitenlänge  eingefügt worden. eingefügt worden.
Jede Ecke des 2. Quadrats berührt je eine Seite des 1. Quadrats.
Das bedeutet, dass im 1. Quadrat das 2. Quadrat ist und noch 4 identlische rechtwinklige Dreiecke mit den Seitenlänge a, b und c.
Wir wissen demnach, dass die Fläche des 1. Quadrats gleich dem Quadrat seiner Seitenlänge ist, also 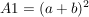 . .
Die Summe der Flächen der 4 Dreiecke und der Fläche des 2. Quadrats entspricht der Fläche des 1. Quadrats 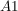 . .
Die Summe dieser Flächen ergibt die folgende Fläche: 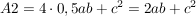
Nun werden die beiden Flächenformeln gleichgesetzt, da 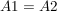 gilt. gilt.
Also:
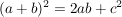
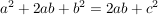 nun wird auf beiden Seiten nun wird auf beiden Seiten 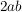 abgezogen abgezogen
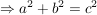
q.e.d (:biggrin:)
siehe auch: ![Link auf "http://de.wikipedia.org/wiki/Dreieck#Das_rechtwinklige_Dreieck" [link]](/images/popup.gif) Wikipedia Wikipedia
|