Regel von Bernoulli und de l HospitalPrämisse
Seien die Funktionen 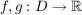 in einer (punktierten) Umgebung von a differenzierbar. in einer (punktierten) Umgebung von a differenzierbar.
Es gelte entweder
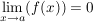 und und 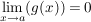
oder
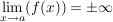 und und 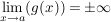
Satz
Existiert der Grenzwert 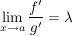 , so gilt auch , so gilt auch 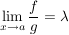 . .
Geltungsbereich
Der Satz gilt sinngemäß für einseitige Grenzwerte und unendlich große a.
Anwendung
Mit dem Satz ist die Darstellung von Grenzwerten wie 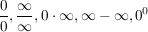 und und 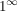 möglich. möglich.
Trivia
Der Satz wird von Studenten auch als "Krankenhausregel" bezeichnet (wegen l'Hospital)
Quelle
Mathematik I für Elektrotechniker,
Vorlesung von PD Dr.-Ing. habil. Dipl.-Math. Klaus Röbenack,
Dresden WS 2006/2007
|