StandardabweichungDie Standardabweichung 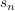 ist ein Streuungsmaß. ist ein Streuungsmaß.
Sie basiert auf der Berechnung der Varianz V(X) einer Zufallsgröße.
Streuungsmaße machen Aussagen darüber, wie weit Messwerte einer Messwertreihe um einen Mittelwert oder von ihrem höchstem zu ihrem niedrigsten Wert streuen.
Die Standardabweichung ist das am häufigsten verwendete Streuungsmaß.
Ich denke, die Definition in der Wikipedia wird dir weiterhelfen:
![Link auf "http://de.wikipedia.org/wiki/Standardabweichung" [link]](/images/popup.gif) Standardabweichung Standardabweichung
Unterscheiden muss man immer zwischen
- der theoretischen Standardabweichung,
die man sich vorgeben kann, z.B. bei Simulationen, oder wenn man einfach annimmt,
dass man eine Normalverteilung mit Standardabweichung 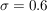 vorliegen hat, vorliegen hat,
- und der empirischen Standardabweichung,
die man aus konkret vorliegenden Daten bestimmt
und damit die theoretische Standardabweichung schätzt:
dabei sind die 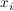 die Werte der zugrunde liegenden Zufallsgröße, die Werte der zugrunde liegenden Zufallsgröße,  der Erwartungswert der Zufallsgröße und der Erwartungswert der Zufallsgröße und  die Anzahl der Zufallswerte. die Anzahl der Zufallswerte.
Im Falle der Normalverteilung gibt es die  -Regeln für die (theoretische) Standardabweichung. Diese findest du bestimmt in deinem Schulbuch. -Regeln für die (theoretische) Standardabweichung. Diese findest du bestimmt in deinem Schulbuch.
Beispiel dafür: Trägt man die Standardabweichung zu beiden Seiten des Mittelwertes auf,
so liegen bei normalverteilten Werten ca. 68% der Werte in diesem Intervall.
Weiterhin wird ![Link auf "http://www.physio-akademie.de/service/wbuch_info.php?bezug=114" [link]](/images/popup.gif) hier mit Worten sehr schön beschrieben, wie man die (empirische) Standardabweichung im Falle konkret vorliegender Daten berechnet. hier mit Worten sehr schön beschrieben, wie man die (empirische) Standardabweichung im Falle konkret vorliegender Daten berechnet.
|