Steighöhe in Kapillare
Die Steighöhe eines Fluids in einer Kapillare
Eine dünne Glaskapillare mit dem Durchmesser d wird in ein Fluid gehalten. Das Fluid steigt in der Kapillaren hoch (Höhe h). Bei bekanntem Benetzungswinkel \Theta kann die Steighöhe berechnet werden.

Wenn R=konst., ergibts sich eine Kugelform und dann steht R senkrecht auf s. Dementsprechend gilt:
Wir nehmen an, dass die Steighöhe links und rechts identisch ist, daher steht h senkrecht auf d, womit gilt:
Daher folgt:
Aus dem Dreick ergibt sich:
Die Young-Laplace-Gleichung sagt aus, dass:
wobei 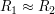 , womit man erhält: , womit man erhält:
Durch zusammenfügen der Gleichungen erhält man:
Unter Betrachtung des hydrostatischen Drucks ergibt sich die Steighöhe zu:
|