LZILZI-GLieder
Verstärkungsprinzip
Liegt ein System mit einem Eingang  und einem Ausgang und einem Ausgang  vor und wird auf den Eingang eine beliebige Größe vor und wird auf den Eingang eine beliebige Größe 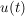 gelegt, dann sei die zugehörige Ausgangsgröße gelegt, dann sei die zugehörige Ausgangsgröße 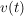 . .
Hat die Multiplikation der Eingangsgröße 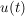 mit einem Faktor c eine ebenso verstärkte Ausgansgröße mit einem Faktor c eine ebenso verstärkte Ausgansgröße 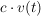 zur Folge, so erfüllt das System das Verstärkungsprinzip. zur Folge, so erfüllt das System das Verstärkungsprinzip.
Überlagerungsprinzip
Werden auf den Eingang  nacheinenander nacheinenander  verschiedene Eingangsgrößen verschiedene Eingangsgrößen 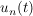 gelegt und am Ausgang gelegt und am Ausgang  als Gesamtsumme die als Gesamtsumme die  Ausgangssignale Ausgangssignale 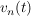 gemessen, erfüllt das System das Überlagerungsprinzip. gemessen, erfüllt das System das Überlagerungsprinzip.
~ Systeme, die das Verstärkungs- und Überlagerungsprinzip erfüllen, heißen "lineare Systeme".
Verschiebungsprinzip
Führt das um 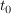 verschobene Eingangssignal verschobene Eingangssignal 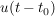 zu einem genauso verschobenen und unverfälschten Ausgangssignal zu einem genauso verschobenen und unverfälschten Ausgangssignal 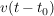 , so erfüllt das System das Verschiebungsprinzip. , so erfüllt das System das Verschiebungsprinzip.
~ Diese Art von Systemen heißen zeitinvariante Systeme.
Lineare zeitinvariante Systeme werden kurz LZI-Glieder genannt. Sie arbeiten meist kontinuierlich, d.h. eine Eingangs- und Ausgangsgröße ist jederzeit gegeben. LZI-Glieder lassen sich durch lineare Differenzialgleichungen beschreiben.
zurück
|