Taylorreihe
Die Taylorreihe an sich
Es sei auf die gute Beschreibung der Wikipedia verwiesen:
![Link auf "http://de.wikipedia.org/wiki/Taylorreihe" [link]](/images/popup.gif) http://de.wikipedia.org/wiki/Taylorreihe http://de.wikipedia.org/wiki/Taylorreihe
Eine einfache Form der Taylorreihe ist die sog. Mc Laurinsche Reihe.
Die Herleitung der Mc Laurinschen Reihe
Grundidee:
Grundidee der Mc Laurinschen Reihe ist es, beliebig oft differenzierbare Funktion 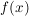 als Potenzreihe darstellen zu können. als Potenzreihe darstellen zu können.

Die Eigenschaft, dass die Funktion beliebig oft differenzierbar ist, kann man sich nun so zu Nutze machen:
Um den Koeffizienten 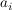 zu erhalten wird die Funktion genau zu erhalten wird die Funktion genau 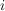 mal differenziert, da dann er Exponent des dazugehörigen mal differenziert, da dann er Exponent des dazugehörigen  auf auf 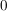 gesunken ist, d.h. gesunken ist, d.h. 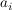 als alleiniges Glied der Summe freisteht. Nun können alle weiteren Glieder der Summe eliminiert werden, indem für als alleiniges Glied der Summe freisteht. Nun können alle weiteren Glieder der Summe eliminiert werden, indem für  der Wert Null eingesetzt wird. Übrig bleibt der Koeffizient der Wert Null eingesetzt wird. Übrig bleibt der Koeffizient 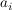 mit dem Faktor mit dem Faktor  , welcher durch das i-fache Ableiten enstanden ist. Wird dieser Ausdruck nun durch , welcher durch das i-fache Ableiten enstanden ist. Wird dieser Ausdruck nun durch  geteilt, so ergibt sich: geteilt, so ergibt sich:

Beispiel:
Der Koeffizient  soll bestimmt werden. soll bestimmt werden.






Die fertige Formel:
Wendet man dieses Prinzip für die Bestimmung eines Koeffizienten auf alle Koeffizienten an, so erhält man für die Mc Laurinsche Reihe der Funktion 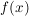 : :

Beispiele:
Die einfachste Mc Laurinsche Reihe ist die der Exponentialfunktion 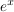 . Da nämlich . Da nämlich  (sprich: die k-te Ableitung der Exponentialfunktion) der Exponentialfunktion entspricht, sich die Funktion also durch die Ableitung nicht ändert, lautet ihre Mc Laurinsche Reihe: (sprich: die k-te Ableitung der Exponentialfunktion) der Exponentialfunktion entspricht, sich die Funktion also durch die Ableitung nicht ändert, lautet ihre Mc Laurinsche Reihe:

Nun zu den trigonometrischen Funktionen:
Kosinus:
 und und 
 und und 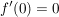
 und und 
 und und 
( ) )
D.h. also, dass wir für ungerade 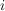 den Koeffizienten nicht zu berechnen brauchen, da den Koeffizienten nicht zu berechnen brauchen, da  ist. ist.
Die Potenzreihendarstellung beinhaltet also nur gerade Exponenten. Die folgen kennt ein Jeder aus dem Schulunterricht: die Kosinusfunktion ist Achsensymmetrisch zur Y-Achse.
Für die noch verbleibenden Glieder der Summe wechselt das Vorzeichen permanent.
Daraus folgt die Mc Laurinsche Reihe für den Kosinus:

Sinus:
 und und 
 und und 
 und und 
 und und 
Im Gegensatz zur Potenzreihendarstellung des Kosinus treten beim Sinus nur ungerade Exponenten auf. Folglich ist die Sinusfunktion punktsymmetrisch zum Ursprung.
Aus der Periodizität der gleich Null gesetzten Ableitungen folgt wie beim Kosinus, nur mit einer kleinen Änderung, die Darstellung der Sinusfunktion als Mc Laurinsche Reihe:

Tangens:
TODO
Kotangens:
TODO
Die Verallgemeinerung: die Taylorreihe
TODO
|