TeilbarkeitsregelSatz Teilbarkeit einer Zahl
Eine Zahl ist teilbar
durch 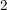 : :
a.) wenn ihre letzte Ziffer durch 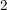 teilbar ist oder teilbar ist oder
b.) wenn ihre letzte Ziffer  ist oder ist oder
c.) wenn die Zahl gerade ist ;-)
durch 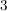 : :
a.) wenn ihre Quersumme durch 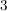 teilbar ist. teilbar ist.
durch 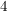 : :
a.) wenn die Zahl gebildet aus den letzten beiden Ziffern durch 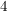 teilbar sind. teilbar sind.
durch 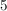 : :
a.) wenn die letzte Ziffer 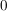 oder oder 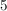 ist. ist.
durch  : :
a.) wenn sie durch 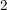 und durch und durch 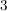 teilbar ist oder teilbar ist oder
b.) wenn ihre letzte Ziffer  ist und ihre Quersumme durch ist und ihre Quersumme durch 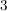 teilbar ist. teilbar ist.
durch  : :
1) Multipliziere die letzte Ziffer der Zahl mit 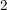
2) Subtrahiere dieses Ergebnis von der Zahl ohne die letzte Stelle
3) Wenn nun das Ergebnis durch  teilbar ist, dann ist es die ursprüngliche Zahl auch teilbar ist, dann ist es die ursprüngliche Zahl auch
Eine auch für große Zahlen wirklich praktikable Teilbarkeitsregel für die 7,
mit der man bei einiger Übung auch Wetten gewinnen kann, indem man z. B. für die Zahl  in der Geschwindigkeit des Hinschreibens berechnen kann, welchen Rest diese Zahl beim Teilen durch in der Geschwindigkeit des Hinschreibens berechnen kann, welchen Rest diese Zahl beim Teilen durch  ergibt, nämlich ergibt, nämlich 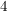 , findet sich hier: http://mathematik.wordpress.com/2007/02/17/eine-praktikable-teilbarkeitsregel-fur-die-7/ , findet sich hier: http://mathematik.wordpress.com/2007/02/17/eine-praktikable-teilbarkeitsregel-fur-die-7/
durch  : :
a.) wenn die Zahl gebildet aus den letzten drei Ziffern durch  teilbar ist. teilbar ist.
durch  : :
a.) wenn die Quersumme der Zahl durch  teilbar ist. teilbar ist.
durch  : :
a.) wenn die letzte Ziffer eine 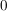 ist. ist.
durch  : :
1) Unterstreiche jede zweite Ziffer der Zahl
2) Addiere die unterstrichenen Zahlen zusammen
3) Addiere danach alle nicht unterstrichenen Zahlen
4) Bilde nun die Differenz der größeren Ziffernsumme minus der kleineren Ziffernsumme
5) Ist das Ergebnis durch  teilbar, dann ist es auch die ursprüngliche Zahl teilbar, dann ist es auch die ursprüngliche Zahl
durch  : :
Eine Zahl ist durch  teilbar, wenn ihre Wechselsumme dritter Stufe durch teilbar, wenn ihre Wechselsumme dritter Stufe durch  teilbar ist teilbar ist
1) Unterstreiche jede zweite Dreiergruppe der Zahl von rechts beginnend
2) Addiere die Zahlen der unterstrichenen Dreiergruppe
3) Addiere die nicht unterstrichenen Zahlen
4) Bilde nun die Differenz der unterstrichenen Zahlengruppe minus der Summe der nicht unterstrichenen Zahlengruppe
5) Ist das Ergebnis durch  teilbar, dann ist es auch die ursprüngliche Zahl teilbar, dann ist es auch die ursprüngliche Zahl
Bemerkungen.
TODO
Beispiele.
Teilbarkeit durch  : :
Beispiel: 
Ziffernsumme der unterstrichenen Zahlen: 
Ziffernsumme der nicht unterstrichenen Zahlen: 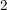
  und und  ist durch ist durch  teilbar teilbar
Das Ergebnis nennt man alternierende Quersumme/Wechselsumme
Teilbarkeit durch  : :
Beispiel:

1) 
2) 
3) 
4) 
5) Das Ergebnis ist nicht durch  teilbar teilbar
anderes Beispiel:

1) 
2) 
3) 
4) 
5)   das Ergebnis ist durch das Ergebnis ist durch  teilbar teilbar
Beweis.
Für die Teilbarkeit durch  : :
Die Zahl sei  . .
 Es existieren Es existieren 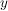 und und  mit mit  . .
Außerdem existieren  und und  mit mit  . .
Also: (1) 
Die einfachere Hilfszahl, deren Teilbarkeit überprüft wird, läßt sich schreiben als
 . .
Auch dort existieren zwei Zahlen  und und  mit mit
(2)  . .
Setze (2) in (1) ein:




Hieraus folgt jetzt, dass  genau dann, wenn genau dann, wenn  . .
(Also: Die ursprüngliche Zahl ist genau dann durch  teilbar ( teilbar ( ), wenn die Hilfszahl durch ), wenn die Hilfszahl durch  teilbar ist ( teilbar ist ( ).) ).)
Eine auch für große Zahlen wirklich praktikable Teilbarkeitsregel für die 7,
mit der man bei einiger Übung auch Wetten gewinnen kann, indem man z. B. für die Zahl 88965321 in der Geschindigkeit des Hinschreibens berechnen kann, welchen Rest diese Zahl beim Teilen durch 7 ergibt, nämlich 4, findet sich hier: http://mathematik.wordpress.com/2007/02/17/eine-praktikable-teilbarkeitsregel-fur-die-7/
|