TeleskopreiheUnter einer (etwa reellen oder komplexen) Teleskopreihe versteht man eine Reihe der Bauart
(Bei einer reellen Teleskopreihe sind alle Summanden rein reell, analog bei einer komplexen alle komplex.)
Es gilt: Aus 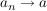 (wobei auch (wobei auch 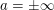 erlaubt sei) folgt erlaubt sei) folgt
(Hinweis: Für 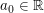 ist ist 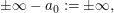 für für 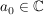 ist ist 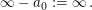 ) )
Beweis:
Es gilt

Weitere Hinweise:
1.) Die Reihe muss nicht zwingend bei 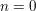 starten. Was sich bei solch einer leichten Modifikation ändert, diese Überlegungen überlassen wir dem mitdenkenden Leser/der mitdenkenden Leserin. starten. Was sich bei solch einer leichten Modifikation ändert, diese Überlegungen überlassen wir dem mitdenkenden Leser/der mitdenkenden Leserin.
2.) Manche Autoren bezeichnen Teleskopreihen auch als Ziehharmonikareihen.
|