Wurzel2Wie beweise ich, dass Wurzel aus 2 eine irrationale Zahl ist?
Grundgedanke des indirekten Beweises:
Annahme: 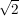 sei eine rationale Zahl, dann lässt sie sich als gekürzten Bruch schreiben: sei eine rationale Zahl, dann lässt sie sich als gekürzten Bruch schreiben: 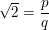 und p, q sind teilerfremd. und p, q sind teilerfremd.
Daraus folgt: 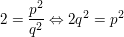 . .
Das heißt, dass 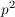 eine gerade Zahl ist, woraus auch folgt, dass p gerade ist, also in der Form eine gerade Zahl ist, woraus auch folgt, dass p gerade ist, also in der Form 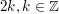 geschrieben werden kann. geschrieben werden kann.
Eingesetzt ergibt das: 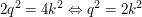 , wodurch auch q gerade sein muss. , wodurch auch q gerade sein muss.
2 ist also Teiler von p und q.
Dies ist aber ein Widerspruch zu der gemachten Annahme!
Daher ist die Annahme als falsch anzusehen: 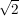 ist irrational! ist irrational!
|