Wurzelrechnungerstes Beispiel:
Wie komme ich bei der Aufgabe
mittels welchem Weg zum Ergebnis 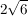 ? ?
Um das zu beantworten, braucht es nur diese 2 Regeln:
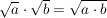 und und 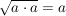
(Hier würde ein strenger Mathematiker zwar sagen, dies sei nicht ganz korrekt: wenn a negativ ist, stimmt es nicht. Für uns genügt das aber vorerst)
Die erste Regel besagt, dass man die Produkte beliebig unter die Wurzel nehmen darf, und auch, wenn man die Regel von rechts nach links liest, dass man Produkte unter einer Wurzel beliebig auseinander nehmen darf, auf verschiedene Wurzeln verteilen.
Nun zu deinem Problem:
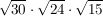
Nach der ersten Regel darf ich schreiben:
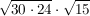
..und weiter: 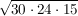
Das hätte man natürlich auch in einem einzigen Schritt machen dürfen!. :-)
Der Trick ist nun der, dass man die Zahlen unter der Wurzel in Faktoren zerlegt:
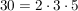
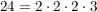
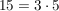
Insgesamt also:
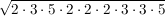
Nun sortieren wir die Faktoren der Grösse nach (ein Mathematiker würde wohl sagen, er wende das Kommutativgesetz an):
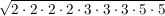
Jetz nehmen wir das wieder geschickt auseinander. Geschickt heisst: wir fassen immer Paare von zwei gleichen Faktoren zusammen:
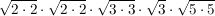
Nun kommt die zweite Regel zur Anwendung:
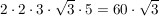
Womit gezeigt ist, dass dein Ergebnis gar nicht stimmt! ;-)
Natürlich darf man auch etwas geschickter vorgehen:
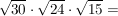
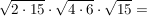
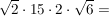
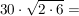
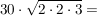
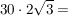
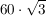
anderes Beispiel:
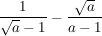
auf den Hauptnenner 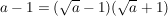 erweitern: erweitern:
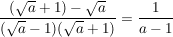
|