abzählbarDefinition abzählbar
Schule
Universität
Eine Menge A heißt (höchstens) abzählbar, wenn es eine surjektive Abbildung 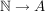 gibt (oder wenn gibt (oder wenn 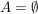 ). ).
A heißt abzählbar unendlich, wenn es eine bijektive Abbildung 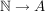 gibt. gibt.
A heißt überabzählbar, wenn A nicht abzählbar ist.
Beispiele
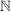 - abzählbar unendlich - abzählbar unendlich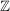 - abzählbar unendlich - abzählbar unendlich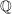 - abzählbar unendlich - abzählbar unendlich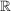 - überabzählbar - überabzählbar
Definition aus dem Meyberg (weicht von obiger leider ab):
Gibt es eine bijektive Abbildung 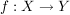 der Menge der Menge 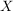 auf die Menge auf die Menge 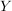 , dann gilt , dann gilt 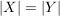 , d.h. die Mengen sind gleichmächtig. Eine Menge heißt abzählbar, wenn es eine bijektive Abbildung , d.h. die Mengen sind gleichmächtig. Eine Menge heißt abzählbar, wenn es eine bijektive Abbildung 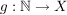 gibt, wenn also gibt, wenn also 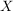 die Mächtigkeit der natürlichen Zahlen hat. die Mächtigkeit der natürlichen Zahlen hat.
Quelle: isbn3446130799
|