halbmetrischer RaumDefinition Halbmetrischer Raum
Es sei X eine nichtleere Menge und es sei 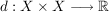 eine Funktion. d heißt Halbmetrik (auf X), falls folgende Bedingungen gelten: eine Funktion. d heißt Halbmetrik (auf X), falls folgende Bedingungen gelten:
d.1) Es gilt d(x,x)=0 für alle 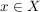 . .
d.2) Es gilt d(x,y)=d(y,x) für alle 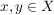 . (Symmetrie) . (Symmetrie)
d.3) Es gilt 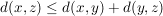 für alle für alle 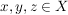 . (Dreiecksungleichung) . (Dreiecksungleichung)
Das Paar (X,d) heißt dann halbmetrischer Raum.
Bemerkungen.
1.) Bei d.1) wird oft zusätzlich 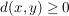 für alle für alle 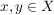 gefordert. Wir werden aber zeigen, dass darauf verzichtet werden kann, denn: gefordert. Wir werden aber zeigen, dass darauf verzichtet werden kann, denn:
Nach d.1) (obige Bedingung!) gilt für alle 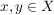 : :
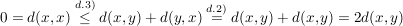 , ,
woraus dann 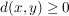 ( (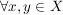 ) folgt. ) folgt. 
2.) Der Unterschied eines halbmetrischen Raumes zu einem metrischen Raum liegt darin, dass es in einem halbmetrischen Raum Elemente 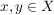 geben kann mit geben kann mit 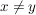 , für die aber d(x,y)=0 gilt. Deswegen sind in einem halbmetrischen Raum die Grenzwerte einer Folge i.A. nicht eindeutig. , für die aber d(x,y)=0 gilt. Deswegen sind in einem halbmetrischen Raum die Grenzwerte einer Folge i.A. nicht eindeutig.
|