liminfDefinition lim inf ("Limes inferior") und lim sup ("Limes superior")
Universität
Sei 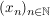 eine Folge. Die Menge H der Häufungspunkte von eine Folge. Die Menge H der Häufungspunkte von 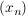 sei beschränkt und nichtleer. sei beschränkt und nichtleer.
Das kleinste Element der Menge H heißt Limes inferior, 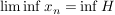 . .
Das größte Element der Menge H heißt Limes superior, 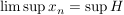 . .
Als alternative Definitionen eignen sich die gekennzeichneten Sätze.
Wichtige Sätze zu Limes inferior und Limes superior
Satz Jede beschränkte Folge reeller Zahlen besitzt einen Limes inferior und einen Limes superior.
(1), Satz 4.G.15
Satz (alternative Definition von liminf und limsup) Sei 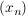 eine beschränkte Folge reeller Zahlen. Dann ist
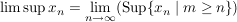
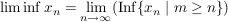
(1), Aufgabe 13 in 4.G
Satz (alternative Definition von liminf und limsup) Sei 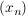 eine beschränkte Folge reeller Zahlen. Dann ist
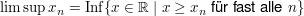
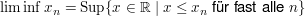
(1), Aufgabe 14 in 4.G
Satz (alternative Definition von liminf und limsup) Sei 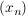 eine beschränkte Folge reeller Zahlen. Dann ist
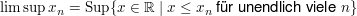
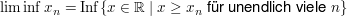
(1), Aufgabe 14 in 4.G
Satz Seien 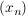 und 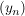 beschränkte Folgen reeller Zahlen.
Es gilt: 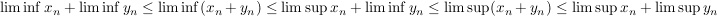
(1), Aufgabe 15a in 4.G
Satz Seien 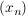 und 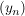 beschränkte Folgen reeller, nichtnegativer Zahlen.
Es gilt: 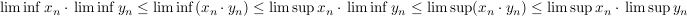
(1), Aufgabe 15b in 4.G
Literaturangaben
(1) isbn3411032049
|