proportionalproportional
Direkte Proportionalität
Die Zuordnung einer direkten Proportionalität hat die Form:
Dabei ist m eine feste Zahl, der Proportionalitätsfaktor.
Betrachtet man 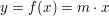 , so erkennt man, dass die Zahlenpaare (x|y) quotientengleich sind; , so erkennt man, dass die Zahlenpaare (x|y) quotientengleich sind;
denn es gilt stets:
Indirekte Proportionalität
Die Zuordnung einer indirekten Proportionalität hat die Form:
Dabei ist a eine feste Zahl, der Proportionalitätsfaktor.
Betrachtet man 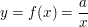 , so erkennt man, dass die Zahlenpaare (x|y) produktgleich sind; , so erkennt man, dass die Zahlenpaare (x|y) produktgleich sind;
denn es gilt stets:
|