verträglichDefinition verträglich
Schule
Universität
Es sei 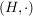 eine Halbgruppe und eine Halbgruppe und 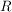 eine Äquivalenzrelation auf eine Äquivalenzrelation auf 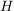 . .
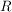 heißt mit der Verknüpfung heißt mit der Verknüpfung  linksverträglich (bzw. rechtsverträglich), wenn für alle linksverträglich (bzw. rechtsverträglich), wenn für alle 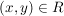 und alle und alle 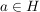 auch auch
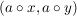 (bzw. (bzw. 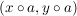 ) )
in 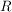 liegen. liegen.
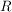 heißt verträglich mit heißt verträglich mit  , wenn , wenn 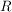 links- und rechtsverträglich ist. links- und rechtsverträglich ist.
Beispiel
Sind 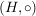 und und 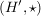 Halbgruppen, Halbgruppen, 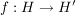 ein Homomorphismus und ein Homomorphismus und
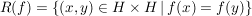 , ,
dann ist 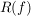 verträglich mit verträglich mit  . .
Quelle: K. Meyberg, Algebra Teil 1, Carl Hanser Verlag, 1980, ISBN 3-446-13079-9
|