ÜbertragungsfunktionÜbertragungsfunktion
Das Übertragungsverhalten eines Systems kann durch eine lineare Differenzialgleichung beschrieben werden:
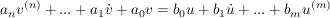
die Laplace-transformierte Gleichung lautet:
![$ V(s)\left[a_ns^n+...+a_1s+a_0\right]=U(s)\left[b_0+b_1s+...+b_ms^m\right] $ $ V(s)\left[a_ns^n+...+a_1s+a_0\right]=U(s)\left[b_0+b_1s+...+b_ms^m\right] $](/teximg/7/7/00444677.png)
Der Quotient 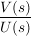 heißt Übertragungsfunktion G(s) heißt Übertragungsfunktion G(s)
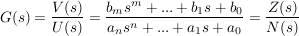
Z(s): Zählerpolynom in s
N(s): Nennerpolynom in s
technisch realisierbar sind Systeme in denen 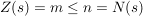
Im Sonderfall m=n lässt sich durch Polynomdivision ein konstanter Anteil abspalten, so dass eine echt gebrochen rationale Funktion
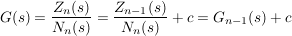
Eine wichtige Beziehung besteht zwischen der Übertragungs- und der Gewichtsfunktion 
Es ist:
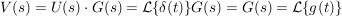
und daher:
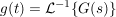
zurück
|