LaplacePierre Simon Marquis de Laplace war ein französicher Physiker, Mathematiker und Astronom, der bereits im 18.Jahrhundert eine detaillierte Darstellung, als Schwerpunkt seiner Forschungsarbeiten, der Entwicklung des Sonnensystems hervorbrachte (Kant-Laplace-Theorie). Daneben beschäftigte er sich unter anderem mit der Integraltheorie und verfasste Arbeiten zur Schwingungs- und Wärmelehre, sowie zur Wahrscheinlichkeitsrechnung.
Nach ihm benannt ist ebenso die Laplace-Gleichung, eine partielle Differenzialgleichung 2. Ordnung mit 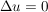
Was bedeutet "Laplace-Transformation"?
Unterwirft man die, mit einem Dämpfungsfaktor (zur Erfüllung der dirichletschen Bedingung) multiplizierte Hilfsfunktion 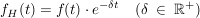 der Fouriertransformation, so ergibt sich als Sonderfall für der Fouriertransformation, so ergibt sich als Sonderfall für 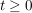
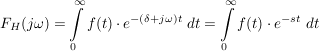
die einseitige Laplace-Transformierte
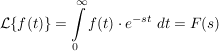 mit mit 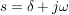
Symbolisch wird für diese Transformation 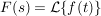 geschrieben. Der Operator geschrieben. Der Operator 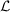 heißt heißt  , F(s) wird die Bildfunktion und f(t) die Zeitfunktion genannt. , F(s) wird die Bildfunktion und f(t) die Zeitfunktion genannt.
Das Laplace-Integral konvergiert, wenn 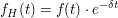 absolut integrierbar ist. Das ist für hinreichend große absolut integrierbar ist. Das ist für hinreichend große 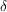 der Fall, wenn f(t) nicht stärker als exponentiell wächst. der Fall, wenn f(t) nicht stärker als exponentiell wächst.
Der kleinste Wert von 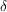 wird minimale Konvergenzabszisse genannt und mit wird minimale Konvergenzabszisse genannt und mit 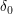 bezeichnet. Das Laplace-Integral konvergiert für alle s, deren Realteil nicht kleiner als bezeichnet. Das Laplace-Integral konvergiert für alle s, deren Realteil nicht kleiner als 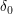 ist. Die Werte von s stellen dann in der komplexen Ebene die Konvergenzhalbebene dar, in welcher die Laplacetransformierte eine reguläre Funktion ist, die über die Konvergenzebene hinaus in den verbleibenden Teil der komplexen Ebene analytisch forgesetzt werden kann (bis auf wenige singuläre Punkte). ist. Die Werte von s stellen dann in der komplexen Ebene die Konvergenzhalbebene dar, in welcher die Laplacetransformierte eine reguläre Funktion ist, die über die Konvergenzebene hinaus in den verbleibenden Teil der komplexen Ebene analytisch forgesetzt werden kann (bis auf wenige singuläre Punkte).
für die Umkehrfunktion benötigt man dann:
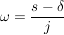
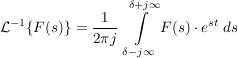
Warum führt man die Laplace-Operation durch?
Unter Zuhilfenahme der Laplace-Transformation wird eine komplizierte Integral- und Differenzialform in eine algebraische Gleichung überführt, die man "leicht" berechnen kann.
Man möge sich jedoch bewusst sein, dass elementare Rechenkenntnisse natürlich Voraussetzung für diese Art der Vereinfachung sind.
Anhand ausgewählter Beispiele soll die Vereinfachung verdeutlicht werden:
Beispiel 1.
Es bestehe ein Netzwerk aus einer Serienschaltung folgender diskreter Bauteile:
ein Ohmscher Widerstand R und ein Kondenator C
nach dem 2. Kirchhoffschen Satz gilt:
u-Ri=0 mit 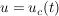 - Kondensatorspannung zur Zeit t; i=i(t) - Stromstärke in Abhängigkeit der Zeit - Kondensatorspannung zur Zeit t; i=i(t) - Stromstärke in Abhängigkeit der Zeit
Es besteht weiterhin folgende lineare Beziehung zwischen der Ladung q=q(t) und der Spannung 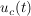 : :
q=Cu und somit gilt nach beiderseitigem differenzieren: 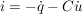
einsetzen in obige Formel ergibt:
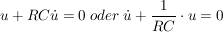
die Lösung der linearen Differenzialgleichung (im folgenden: "Dgl") ergibt sich mit: 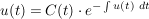
mit der Anfangsbedingung 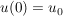 erhalten wir erhalten wir 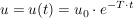 für für 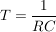
Diese Rechnung setzt die Kenntnisse der Integral- und Differenzialrechnung voraus.
nun dasselbe Beispiel mit der Laplace-Transformation:
Unter Anwedung der gliedweisen Transformation auf die Differenzialgleichung wird:
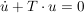 zu zu 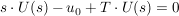
aufglöst nach U(s):
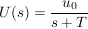
Aus der Korrespondenztabelle lässt sich sofort 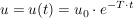 ablesen. ablesen.
Das Verhalten eines 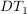 -Regelkreisgliedes lässt sich durch -Regelkreisgliedes lässt sich durch
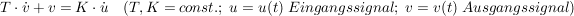
beschreiben.
Es sei 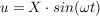 das Eingangssignal mit dem Anfangswert v(0)=0 das Eingangssignal mit dem Anfangswert v(0)=0
mit 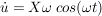 lautet die Dgl: lautet die Dgl:
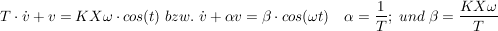
die Transformation bringt:
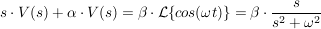
somit folgt für V(s):
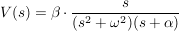
Für die Rücktransformation (z.B. mittels des Faltungssatzes) bekommen wir als Orginalfunktion:
![$ v(t)=\bruch{KX\omega}{1+(\omega t)^2}\cdot{}\left[cos(\omega t)+\omega T\cdot{}sin(\omega t)-e^{-\bruch{t}{T}}\right] $ $ v(t)=\bruch{KX\omega}{1+(\omega t)^2}\cdot{}\left[cos(\omega t)+\omega T\cdot{}sin(\omega t)-e^{-\bruch{t}{T}}\right] $](/teximg/4/7/00448474.png)
Beispiel 3: Lösung einer DGL
Exemplarische Lösung einer inhomogenen Differenzialgleichung der 2. Ordnung
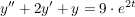 mit folgenden Anfangswerten y(0)=0 und mit folgenden Anfangswerten y(0)=0 und 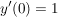
Die Transformation unter Anwendung des Ableitungsatzes in den Bildraum ergibt sich zu:
![$ [s^2\cdot{}Y(s)-s\cdot{}y(0)-y'(0)]+2\cdot{}s\cdot{}Y(s)+Y(s)=\bruch{9}{s-2} $ $ [s^2\cdot{}Y(s)-s\cdot{}y(0)-y'(0)]+2\cdot{}s\cdot{}Y(s)+Y(s)=\bruch{9}{s-2} $](/teximg/1/9/01407691.png)
Nach dem Einsetzen der Anfangswerte wird die Gleichung nach Y(s) aufgelöst
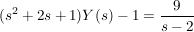
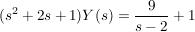
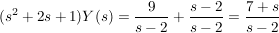
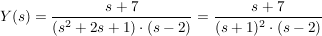
Partialbruchzerlegung
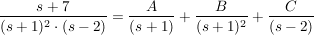
A=-1
B=-2
C=1
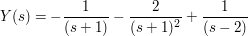
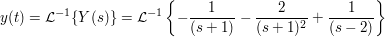
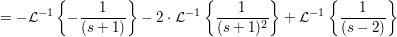
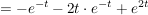
Anm: die Bespiele sind in stark verkürzter Form dargestellt und beinhalten keine Rechenwege; ausführliche Beispiele sind in den u.a. einzelnen Kapiteln zu finden.
Eigenschaften der Laplace-Transformation:
Laplace-Linearität (Satz über Linearkombinationen)
Laplace-Ähnlichkeitssatz
Laplace-Verschiebungssatz
Laplace-Dämpfungssatz
Laplace-Ableitungssatz
Laplace-Integralsatz
Laplace-Faltungssatz
Laplace-Grenzwertsatz
Laplace-Periodische Funktionen
Laplace-Rücktransformation
Laplace-Anwendungen
Laplace-Korrespondenztabelle
Elementare Funktionen
Laplacetransformation elementarer Funktionen
|