Vorhilfe Kostenlose Kommunikationsplattform für gegenseitige Hilfestellungen.
	Hallo Gast! [ einloggen \| registrieren ]
	Startseite · Forum · Wissen · Kurse · Mitglieder · Team · Impressum

Navigation

Startseite...
Neuerdings beta neu
Forum...
vorwissen
	Einstieg

	Index aller Artikel

	Hilfe / Dokumentation
	Richtlinien
	Textgestaltung
vorkurse...
Werkzeuge...
Nachhilfevermittlung beta...
Online-Spiele beta
Suchen
Verein...
Impressum

Das Projekt

Server und Internetanbindung werden durch Spenden finanziert.

Organisiert wird das Projekt von unserem Koordinatorenteam.

Hunderte Mitglieder helfen ehrenamtlich in unseren moderierten Foren.

Anbieter der Seite ist der gemeinnützige Verein "Vorhilfe.de e.V.".

Partnerseiten

Weitere Fächer:

Vorhilfe.de

FunkyPlot: Kostenloser und quelloffener Funktionenplotter für Linux und andere Betriebssysteme

Laplace-Periodische_Funktionen

Mach mit! und verbessere/erweitere diesen Artikel!

Artikel • Seite bearbeiten • Versionen/Autoren

Laplace-Periodische Funktionen

Laplacetransformierte der Sinusfunktion

Mit der Beziehung 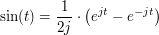$\sin(t)=\bruch{1}{2j}\cdot{}\big(e^{jt}-e^{-jt}\big)$ und unter Ausnutzung der Linearitätsregelergibt sich für die L-Transformierte

$\mathcal{L}\{\sin(t)\}=\mathcal{L}\left\{\bruch{1}{2j}\left(e^{jt}-e^{-jt}\right)\right\}=\bruch{1}{2j}\mathcal{L}\left\{e^{jt}\right\}-\bruch{1}{2j}\mathcal{L}\left\{e^{-jt}\right\}$

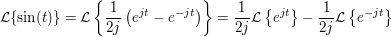
wegen der Laplacetransformation der e-Funktion erhält man sofort

$\mathcal{L}\{\sin(t)\}=\bruch{1}{2j}\cdot{}\bruch{1}{s-j}-\bruch{1}{2j}\cdot{}\bruch{1}{s+j}=\bruch{1}{s^2+1}$

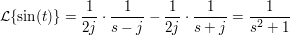
zurück zur Einführung: Laplace

Erstellt: Fr 16.02.2007 von Herby

Letzte Änderung: Fr 12.02.2010 um 06:35 von Herby

Artikel • Seite bearbeiten • Versionen/Autoren • Titel ändern • Artikel löschen • Quelltext