Laplacetransformation (elementare Funktionen)(1) Die Laplace-Transformation der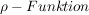 
Der Einheitssprung sei definiert durch:
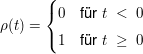
da 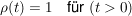 gilt, ergibt sich die L-Transformierte zu
![$ \mathcal{L}\left\{\rho (t)\right\}=\integral_{t=0}^{\infty}{\rho(t)\cdot{}e^{-st}\ dt}=\integral_{t=0}^{\infty}{1\cdot{}e^{-st}\dt}=\left[-\bruch{1}{s}\cdot{}e^{-st}\right]_{t=0}^{\infty}=\bruch{1}{s} $](/teximg/5/5/01407655.png "$ \mathcal{L}\left\{\rho (t)\right\}=\integral_{t=0}^{\infty}{\rho(t)\cdot{}e^{-st}\ dt}=\integral_{t=0}^{\infty}{1\cdot{}e^{-st}\dt}=\left[-\bruch{1}{s}\cdot{}e^{-st}\right]_{t=0}^{\infty}=\bruch{1}{s} $")
(2) Die Laplace-Transformation der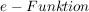 
Die Transformierte lautet mit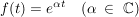 
![$ \mathcal{L}\left\{e^{\alpha(t)}\right\}=\integral_{t=0}^{\infty}{e^{\alpha t}\cdot{}e^{-st}\ dt}=\integral_{t=0}^{\infty}{e^{-(s-\alpha)t}\ dt}=\left[-\bruch{1}{(s-a)}\cdot{}e^{-(s-a)t}\right]_{t=0}^{\infty}=\frac1{s-a} $](/teximg/7/5/01407657.png "$ \mathcal{L}\left\{e^{\alpha(t)}\right\}=\integral_{t=0}^{\infty}{e^{\alpha t}\cdot{}e^{-st}\ dt}=\integral_{t=0}^{\infty}{e^{-(s-\alpha)t}\ dt}=\left[-\bruch{1}{(s-a)}\cdot{}e^{-(s-a)t}\right]_{t=0}^{\infty}=\frac1{s-a} $")
(3) Die Laplace-Transformation der Rampenfunktion
(4) Die Laplace-Transformation der Rechteckfunktion
(5) Die Laplace-Transformierte der Sinusfunktion
Die Sinusfunktion sei definiert durch:
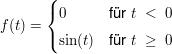
Unter Anwendung der partiellen Integration folgt für die L-Transformierte
![$ \mathcal{L}\{\sin(t)\}=\integral^{\infty}_{t=0}{\sin{t}\cdot{}e^{-st}\ dt}=\left[-\bruch{e^{-st}}{s^2+1}\cdot{}(s\cdot{}\sin(t)+\cos(t)\right]_{t=0}^{\infty}=\frac1{s^2+1} $](/teximg/6/4/01407846.png "$ \mathcal{L}\{\sin(t)\}=\integral^{\infty}_{t=0}{\sin{t}\cdot{}e^{-st}\ dt}=\left[-\bruch{e^{-st}}{s^2+1}\cdot{}(s\cdot{}\sin(t)+\cos(t)\right]_{t=0}^{\infty}=\frac1{s^2+1} $")
zur Einführung der Laplacetransformation
| 
