AutomorphismengruppeDefinition Automorphismengruppe
Universität
Es sei  eine Gruppe. Einen Isomorphismus (also ein bijektiver Gruppenhomomorphismus) von eine Gruppe. Einen Isomorphismus (also ein bijektiver Gruppenhomomorphismus) von  auf sich nennt man einen Automorphismus von auf sich nennt man einen Automorphismus von  . .
Die Grundlage zur Definition der Automorphismengruppe bilden die folgenden Aussagen über Gruppenhomomorphismen
a) Sind 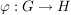 und und 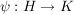 Homomorphismen von Gruppen, dann ist auch Homomorphismen von Gruppen, dann ist auch 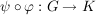 ein Homomorphismus. ein Homomorphismus.
b) Ist 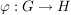 ein Isomorphismus, dann ist auch ein Isomorphismus, dann ist auch 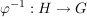 ein Isomorphismus. ein Isomorphismus.
c) Sind 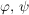 Isomorphismen, so auch Isomorphismen, so auch 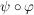 . .
d) Die Identität 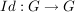 , , 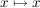 , ist ein Automorphismus. , ist ein Automorphismus.
Es sei nun
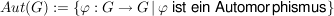 . .
Nach den obigen Aussagen gilt mit 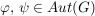 auch auch 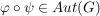 , , 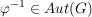 und und 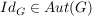 . Da die Komposition von Abbildungen stets assoziativ ist, ist . Da die Komposition von Abbildungen stets assoziativ ist, ist 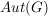 zusammen mit zusammen mit 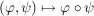 eine Gruppe. Sie heißt die Automorphismengruppe von eine Gruppe. Sie heißt die Automorphismengruppe von  . .
Quelle: isbn3446130799
|