Benutzer:tobit09/Beweis-Anleitung Beispiel-surjektivWie führe ich einen Beweis?
 d) Gruppe d) Gruppe  5. Beispiele 5. Beispiele  f) Injektivität, Bilder und Urbilder f) Injektivität, Bilder und Urbilder
5. Beispiele
e) Surjektivität
Aufgabe:
Seien X,Y und Z Mengen. Seien 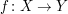 und und 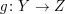 beide surjektiv. Zeigen Sie, dass dann auch beide surjektiv. Zeigen Sie, dass dann auch 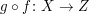 surjektiv ist. surjektiv ist.
Vorbereitung des Beweises:
Voraussetzungen:
"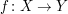 surjektiv" bedeutet: surjektiv" bedeutet:
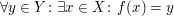 . .
"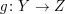 surjektiv" bedeutet: surjektiv" bedeutet:
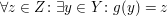 . .
Behauptung:
"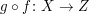 surjektiv" bedeutet: surjektiv" bedeutet:
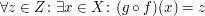 . .
Darin bedeutet 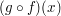 nach Definition der Verkettung nach Definition der Verkettung  von Abbildungen gerade von Abbildungen gerade 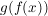 . .
Rahmen des Beweises:
Zu zeigen ist also eine "für alle"-Aussage. Punkt f) unter 3. Wie zeige ich...? verrät uns, was zu tun ist: Wir betrachten ein beliebig vorgegebenes Element 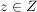 und zeigen unter der zusätzlichen Voraussetzung und zeigen unter der zusätzlichen Voraussetzung 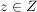 die Aussage die Aussage
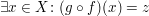 . .
Zu zeigen ist also nun eine "es existiert"-Aussage. Punkt g) unter 3. Wie zeige ich...? verrät uns, was zu tun ist: Wir müssen ein Beispiel-Element 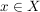 finden, für das finden, für das 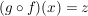 gilt. gilt.
Somit ergibt sich folgender Beweisrahmen:
Zu zeigen ist, dass 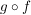 surjektiv ist, d.h. dass für alle surjektiv ist, d.h. dass für alle 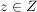 ein ein 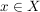 mit mit 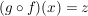 existiert. existiert.
Sei also 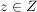 . .
Zu zeigen ist, dass ein 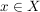 existiert mit existiert mit 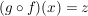 . .
...
Hauptteil
(Finden eines Beispiel-Elementes 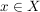 .) .)
(Nachweis von 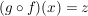 für dieses Beispiel-Element.) für dieses Beispiel-Element.)
...
Somit ist die Existenz eines 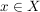 mit mit 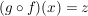 nachgewiesen. nachgewiesen.
Da 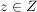 beliebig war, folgt, dass für alle beliebig war, folgt, dass für alle 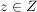 ein ein 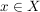 existiert mit existiert mit 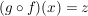 . .
Also ist 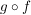 tatsächlich surjektiv. tatsächlich surjektiv.
Hauptteil des Beweises:
Die Voraussetzungen sind "für alle"-Aussagen. In 4. Wie benutze ich...? erfahren wir unter Punkt f), wie wir sie ins Spiel bringe können: Wir benötigen ein Element 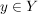 , um auf die Existenz eines , um auf die Existenz eines 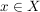 mit mit 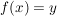 schließen zu können bzw. ein schließen zu können bzw. ein 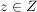 , um auf die Existenz eines , um auf die Existenz eines 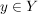 mit mit 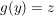 schließen zu können. Ein schließen zu können. Ein 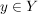 haben wir nicht, aber ein haben wir nicht, aber ein 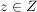 haben wir in der Situation des Hauptteils. Wenden wir also die Voraussetzung, dass haben wir in der Situation des Hauptteils. Wenden wir also die Voraussetzung, dass 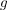 surjektiv ist, auf dieses surjektiv ist, auf dieses  an: Wir erhalten die Aussage an: Wir erhalten die Aussage
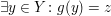 . .
Unter Punkt g) in 4. Wie benutze ich...? erfahren wir, wie wir diese neue Aussage nutzen können: Wir können nun unter der zusätzlichen Voraussetzung, dass wir ein 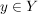 mit mit 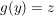 gegeben haben, weiter argumentieren. Und das passt gut: Denn genau ein gegeben haben, weiter argumentieren. Und das passt gut: Denn genau ein 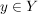 brauchten wir ja, um die Surjektivität von brauchten wir ja, um die Surjektivität von 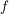 ins Spiel bringen zu können. Wenden wir also die Surjektivität von ins Spiel bringen zu können. Wenden wir also die Surjektivität von 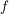 auf unser auf unser 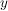 an: Wir erhalten die Aussage an: Wir erhalten die Aussage
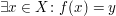 . .
Wir können also nun unter der zusätzlichen Voraussetzung, dass wir ein 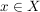 mit mit 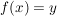 gegeben haben, weiter argumentieren. Insbesondere haben wir ein Beispiel-Element gegeben haben, weiter argumentieren. Insbesondere haben wir ein Beispiel-Element 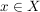 gefunden. gefunden.
Bleibt noch nachzuweisen, dass dieses Element  die Aussage die Aussage 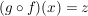 erfüllt. Dazu hilft uns die Definition von erfüllt. Dazu hilft uns die Definition von 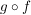 , die Eigenschaft , die Eigenschaft 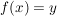 und die Eigenschaft und die Eigenschaft 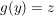 : :
Es gilt 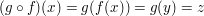 . .
Fertiger Beweis:
Zu zeigen ist, dass 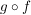 surjektiv ist, d.h. dass für alle surjektiv ist, d.h. dass für alle 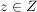 ein ein 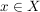 mit mit 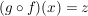 existiert. existiert.
Sei also 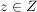 . .
Zu zeigen ist, dass ein 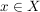 existiert mit existiert mit 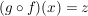 . .
Wegen der Surjektivität von 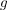 existiert ein existiert ein 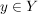 mit mit 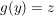 . .
Wegen der Surjektivität von 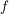 existiert ein existiert ein 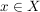 mit mit 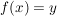 . .
Es gilt 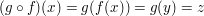 . .
Somit ist die Existenz eines 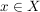 mit mit 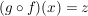 nachgewiesen. nachgewiesen.
Da 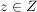 beliebig war, folgt, dass für alle beliebig war, folgt, dass für alle 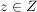 ein ein 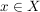 existiert mit existiert mit 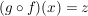 . .
Also ist 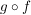 tatsächlich surjektiv. tatsächlich surjektiv.
|