Benutzer:tobit09/Beweis-Tutorial A16Beweis-Tutorial
 4. "für alle"-Aussagen 4. "für alle"-Aussagen
Lösungsvorschlag Aufgabe 16
Aufgabe:
Zeige, dass für alle reellen Zahlen  mit mit 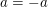 stets stets 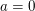 gilt. gilt.
Überlegungen zur Lösung:
Übliches Vorgehen zum Nachweis der zu zeigenden "für alle"-Aussage:
Wir betrachten also eine beliebig vorgegebene reelle Zahl 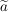 mit mit 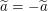 und wollen und wollen 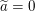 zeigen. zeigen.
Tatsächlich können wir 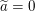 aus der Gleichung aus der Gleichung 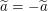 mittels Äquivalenzumformungen folgern, wie der unten stehende Beweis zeigt. mittels Äquivalenzumformungen folgern, wie der unten stehende Beweis zeigt.
Lösungsvorschlag:
Sei 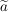 eine reelle Zahl mit eine reelle Zahl mit  . Dann folgt aus dieser Gleichung durch Addition von . Dann folgt aus dieser Gleichung durch Addition von 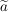 auf beiden Seiten auf beiden Seiten  , also , also  . Mittels Division durch . Mittels Division durch  folgt folgt 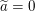 . .
Da 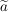 mit mit 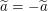 beliebig war, gilt somit beliebig war, gilt somit 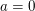 für alle reellen Zahlen für alle reellen Zahlen  mit mit 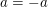 . .
|