Benutzer:tobit09/Beweis-Tutorial alleBeweis-Tutorial
 2. "es existiert"-Aussagen 2. "es existiert"-Aussagen  Inhaltsverzeichnis Inhaltsverzeichnis
3. "für alle"-Aussagen
Wie zeige ich eine "für alle"-Aussage?
Beispiel Die Funktion 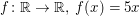 ist monoton steigend. ist monoton steigend.
Zu zeigen ist also nach Definition von "monoton steigend": Für alle reellen Zahlen  und und  mit mit  gilt gilt 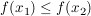 . .
Eine Möglichkeit, eine solche "für alle"-Aussage zu zeigen, ist die folgende: Wir betrachten "beliebig vorgegebene" Zahlen  und und  mit mit 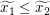 . Dann zeigen wir, dass für diese Zahlen . Dann zeigen wir, dass für diese Zahlen 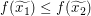 gilt. Da gilt. Da  und und  mit mit 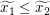 beliebig vorgegeben waren, gilt somit beliebig vorgegeben waren, gilt somit 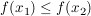 für ALLE reellen Zahlen für ALLE reellen Zahlen  und und  mit mit  . Diese Vorgehensweise können wir mit folgendem "Beweis-Rahmen" notieren: . Diese Vorgehensweise können wir mit folgendem "Beweis-Rahmen" notieren:
Seien  und und  beliebig vorgegebene reelle Zahlen mit beliebig vorgegebene reelle Zahlen mit 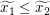 . .
...
Also gilt 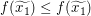 . .
Da  und und  mit mit 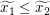 beliebig vorgegeben waren, gilt somit beliebig vorgegeben waren, gilt somit 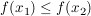 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  . .
Also ist 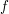 monoton steigend. monoton steigend.
Ergänzen wir nun noch den fehlenden Teil: Wir sind also in der Situation, reelle Zahlen  und und  mit mit 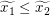 vorgegeben zu haben, und müssen vorgegeben zu haben, und müssen 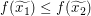 zeigen. Wegen zeigen. Wegen 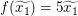 und und 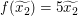 müssen wir also müssen wir also 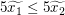 zeigen. Dies folgt jedoch direkt aus zeigen. Dies folgt jedoch direkt aus 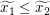 und und 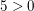 (Ungleichungen bleiben bei Multiplikation mit einer positiven Zahl erhalten). Unseren fertigen Beweis können wir nun wie folgt notieren: (Ungleichungen bleiben bei Multiplikation mit einer positiven Zahl erhalten). Unseren fertigen Beweis können wir nun wie folgt notieren:
Seien  und und  beliebig vorgegebene reelle Zahlen mit beliebig vorgegebene reelle Zahlen mit 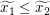 . .
Wegen 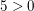 gilt dann auch gilt dann auch 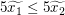 . .
Also gilt 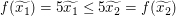 . .
Da  und und  mit mit 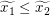 beliebig vorgegeben waren, gilt somit beliebig vorgegeben waren, gilt somit 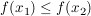 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  . .
Also ist 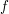 monoton steigend. monoton steigend.
Eine Bemerkung noch: Bei diesem elementaren Beispiel hätten wir auch einfach schreiben können:
"Für alle reellen Zahlen  und und  mit mit  gilt unter Beachtung von gilt unter Beachtung von 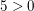 : : 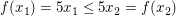 . Also ist . Also ist 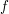 monoton steigend." monoton steigend."
Bei komplexeren Beispielen, wie wir sie noch kennenlernen werden, ist eine solche Kurzfassung jedoch nicht mehr möglich. Daher haben wir gleich die in den meisten Fällen anwendbare Methode vorgestellt. Auch beim Bearbeiten der folgenden Übungsaufgaben solltest du auf eine Kurzfassung verzichten, um die später benötigte Methode bereits an einfacheren Beispielen einzuüben.
Aufgabe 14 Zeige, dass die Funktion 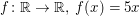 ungerade ist. Lösungsvorschlag ungerade ist. Lösungsvorschlag
Aufgabe 15 Zeige, dass die Funktion 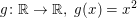 gerade ist. Lösungsvorschlag gerade ist. Lösungsvorschlag
Aufgabe 16 Zeige, dass für alle reellen Zahlen  mit mit 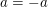 stets stets 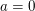 gilt. Lösungsvorschlag gilt. Lösungsvorschlag
Wie benutze ich eine "für alle"-Aussage?
Starten wir mal damit, die Aussage
"Für alle Leserinnen und Leser 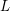 dieses Tutorials gilt: dieses Tutorials gilt: 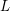 will etwas lernen." will etwas lernen."
als wahr anzunehmen. Was können wir daraus schließen? Z.B., dass du etwas lernen möchtest! Denn du bist eine Leserin oder ein Leser dieses Tutorials.
Allgemeiner: Wenn wir irgendeine Aussage (im Beispiel: "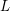 will etwas lernen") für alle "Objekte" einer gewissen Art (im Beispiel: für alle Leserinnen und Leser will etwas lernen") für alle "Objekte" einer gewissen Art (im Beispiel: für alle Leserinnen und Leser 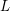 dieses Tutorials) gegeben haben, können wir daraus einen sinnvollen Schluss ziehen, sobald wir ein Objekt dieser Art (im Beispiel: dich) vorliegen haben: Was für alle Objekte dieser Art gilt, gilt insbesondere für das vorliegende Objekt dieser Art. dieses Tutorials) gegeben haben, können wir daraus einen sinnvollen Schluss ziehen, sobald wir ein Objekt dieser Art (im Beispiel: dich) vorliegen haben: Was für alle Objekte dieser Art gilt, gilt insbesondere für das vorliegende Objekt dieser Art.
Wenden wir uns nun einem etwas mathematischeren Beispiel zu:
Beispiel Sei  eine monoton steigende Funktion. Dann ist auch die Funktion eine monoton steigende Funktion. Dann ist auch die Funktion 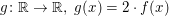 monoton steigend. monoton steigend.
Unsere übliche "Vorab-Analyse":
Gegeben:
eine Funktion 
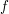 monoton steigend, d.h. monoton steigend, d.h. 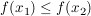 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit 
die Funktion 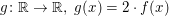
Zu zeigen:
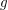 monoton steigend, d.h. monoton steigend, d.h. 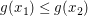 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  . .
Wie unser Beweis-Rahmen aussehen wird, wissen wir schon: Wir betrachten beliebig vorgegebene reelle Zahlen  und und  mit mit 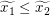 und wollen und wollen 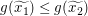 zeigen. Da zeigen. Da  und und  beliebig vorgegeben waren, gilt dann in der Tat beliebig vorgegeben waren, gilt dann in der Tat 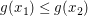 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  . Fehlt noch der Hauptteil: Wir sind in der Situation, reelle Zahlen . Fehlt noch der Hauptteil: Wir sind in der Situation, reelle Zahlen  und und  mit mit 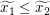 vorgegeben zu haben und müssen vorgegeben zu haben und müssen 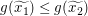 zeigen. Wegen zeigen. Wegen 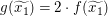 und und 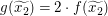 müssen wir also müssen wir also 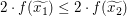 zeigen. zeigen.
Nun haben wir gegeben, dass 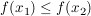 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  gilt. Also gilt dies insbesondere für unsere Zahlen gilt. Also gilt dies insbesondere für unsere Zahlen  und und  (denn (denn  und und  sind reelle Zahlen mit sind reelle Zahlen mit 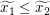 ): Wir erhalten ): Wir erhalten 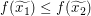 . Wegen . Wegen 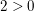 folgt aus folgt aus 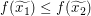 , dass wie gewünscht auch , dass wie gewünscht auch 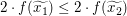 gilt. gilt.
Unser Beweis im Zusammenhang:
Seien  und und  beliebig vorgegebene reelle Zahlen mit beliebig vorgegebene reelle Zahlen mit 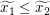 . .
Da 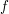 monoton steigend ist, gilt monoton steigend ist, gilt 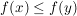 für alle reellen Zahlen für alle reellen Zahlen  und und 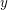 mit mit 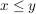 . .
Da  und und  reelle Zahlen mit reelle Zahlen mit 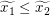 sind, gilt somit insbesondere sind, gilt somit insbesondere 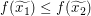 . .
Wegen 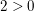 folgt folgt 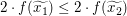 . .
Also 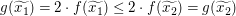 . .
Da  und und  beliebig vorgegeben waren, gilt somit beliebig vorgegeben waren, gilt somit 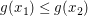 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  . .
Also ist 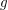 monoton steigend. monoton steigend.
Aufgabe 17 Sei  eine gerade Funktion. Zeige, dass dann auch die Funktion eine gerade Funktion. Zeige, dass dann auch die Funktion 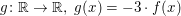 gerade ist. Lösungsvorschlag gerade ist. Lösungsvorschlag
Beispiel Sei  eine monoton steigende Funktion. Dann ist die Funktion eine monoton steigende Funktion. Dann ist die Funktion 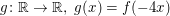 monoton fallend. monoton fallend.
Gegeben:
eine Funktion 
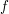 monoton steigend, d.h. monoton steigend, d.h. 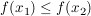 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit 
die Funktion 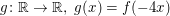
Zu zeigen:
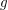 monoton fallend, d.h monoton fallend, d.h 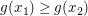 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit 
Seien  und und  beliebig vorgegebene reelle Zahlen mit beliebig vorgegebene reelle Zahlen mit 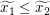 . Zu zeigen ist . Zu zeigen ist 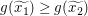 . .
Wegen 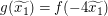 und und 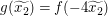 ist also ist also 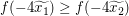 zu zeigen. zu zeigen.
Wir könnten nun wie im vorherigen Beispiel die gegebene Aussage 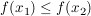 auf auf  und und  anwenden. Dann erhielten wir anwenden. Dann erhielten wir 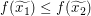 . Nur leider hilft uns das beim Nachweis von . Nur leider hilft uns das beim Nachweis von 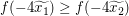 nicht weiter. nicht weiter.
Wir benötigen stattdessen eine Ungleichung über die Funktionswerte von 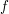 an den Stellen an den Stellen 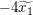 und und 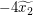 . Also hilft es uns vielleicht weiter, die gegebene Aussage . Also hilft es uns vielleicht weiter, die gegebene Aussage 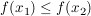 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  anzuwenden auf anzuwenden auf 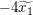 und und 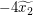 . Dazu benötigen wir das Wissen, welche der beiden letztgenannten Zahlen kleiner gleich der anderen ist. Wegen . Dazu benötigen wir das Wissen, welche der beiden letztgenannten Zahlen kleiner gleich der anderen ist. Wegen 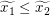 und und 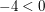 gilt gilt 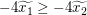 ("bei Multiplikation beider Seiten einer Ungleichung mit einer negativen Zahl kehrt sich das Ungleichheitszeichen um"), also ("bei Multiplikation beider Seiten einer Ungleichung mit einer negativen Zahl kehrt sich das Ungleichheitszeichen um"), also 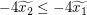 . Daher können wir nun tatsächlich die Aussage . Daher können wir nun tatsächlich die Aussage 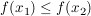 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  auf diese beiden Zahlen auf diese beiden Zahlen 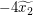 und und 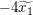 anwenden: Wir erhalten anwenden: Wir erhalten 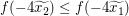 . .
Also haben wir wie gewünscht 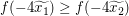 gezeigt! Schreiben wir nun unsere Argumentation sauber auf: gezeigt! Schreiben wir nun unsere Argumentation sauber auf:
Seien  und und  beliebig vorgegebene reelle Zahlen mit beliebig vorgegebene reelle Zahlen mit 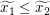 . .
Wegen 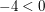 folgt folgt 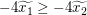 , also gilt , also gilt 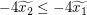 . .
Da 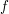 monoton steigend ist, gilt monoton steigend ist, gilt 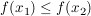 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  . .
Insbesondere gilt wegen 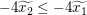 die Ungleichung die Ungleichung 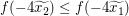 . .
Es folgt 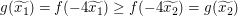 . .
Da  und und  mit mit 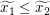 beliebig waren, gilt somit beliebig waren, gilt somit 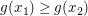 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  . .
Also ist 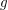 monoton fallend. monoton fallend.
Nachdem wir nun hoffentlich halbwegs vertraut mit den vorgestellten Standard-Schlussweisen für "für alle"-Aussagen sind, möchte ich am gerade behandelten Beispiel alternative Möglichkeiten vorstellen, solche Beweise zu notieren. Natürlich gibt es noch viel mehr Varianten. Eine Möglichkeit:
Zu zeigen ist, dass 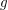 monoton fallend ist, d.h. dass monoton fallend ist, d.h. dass 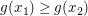 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  gilt. gilt.
Seien also  und und  beliebig vorgegebene reelle Zahlen mit beliebig vorgegebene reelle Zahlen mit 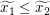 . Zu zeigen ist . Zu zeigen ist 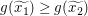 . .
Aus 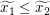 folgt wegen folgt wegen 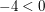 die Ungleichung die Ungleichung 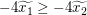 , also , also 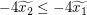 . .
Da 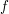 monoton steigend ist, gilt monoton steigend ist, gilt 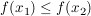 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  . .
Insbesondere gilt wegen 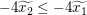 die Ungleichung die Ungleichung 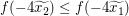 . .
Es folgt 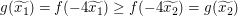 , was zu zeigen war. , was zu zeigen war.
Diese Schreibweise hat den Vorteil, dass von Anfang an die Struktur des Beweises transparent wird. Daher werden wir sie in den Beispielen der folgenden Seiten und ab jetzt in den Lösungsvorschlägen nutzen. Wenn man möchte, kann man die Argumentation auch etwas knapper formulieren:
Seien  und und  reelle Zahlen mit reelle Zahlen mit 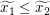 . Zu zeigen ist . Zu zeigen ist 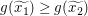 . .
Aus 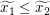 folgt wegen folgt wegen 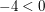 die Ungleichung die Ungleichung 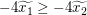 , also , also 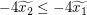 . .
Da 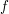 monoton steigend ist, gilt somit monoton steigend ist, gilt somit 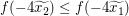 . .
Es folgt 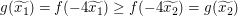 . .
Aufgabe 18 Sei  eine monoton fallende Funktion. Seien eine monoton fallende Funktion. Seien  und und 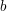 reelle Zahlen. Zeige, dass auch die Funktion reelle Zahlen. Zeige, dass auch die Funktion 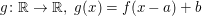 monoton fallend ist. Lösungsvorschlag monoton fallend ist. Lösungsvorschlag
Aufgabe 19 Seien  und und 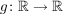 monoton steigende Funktionen. Zeige, dass dann auch die Funktion monoton steigende Funktionen. Zeige, dass dann auch die Funktion 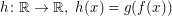 monoton steigend ist. Lösungsvorschlag monoton steigend ist. Lösungsvorschlag
Aufgabe 20 Sei  eine Funktion, die sowohl gerade als auch ungerade ist. Zeige eine Funktion, die sowohl gerade als auch ungerade ist. Zeige 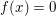 für alle reellen Zahlen für alle reellen Zahlen  . (Tipp: Gemäß Aufgabe 16 gilt: Für alle reellen Zahlen . (Tipp: Gemäß Aufgabe 16 gilt: Für alle reellen Zahlen  mit mit 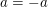 gilt gilt 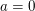 .) Lösungsvorschlag .) Lösungsvorschlag
|