Benutzer:tobit09/Beweis-Tutorial A18Beweis-Tutorial
 4. "für alle"-Aussagen 4. "für alle"-Aussagen
Lösungsvorschlag Aufgabe 18
Aufgabe:
Sei  eine monoton fallende Funktion. Seien eine monoton fallende Funktion. Seien  und und 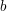 reelle Zahlen. Zeige, dass auch die Funktion reelle Zahlen. Zeige, dass auch die Funktion 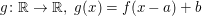 monoton fallend ist. monoton fallend ist.
Überlegungen zur Lösung:
Gegeben:
eine Funktion 
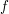 monoton fallend, d.h. monoton fallend, d.h. 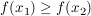 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  . .
die Funktion 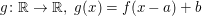
Zu zeigen:
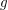 monoton fallend, d.h. monoton fallend, d.h. 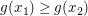 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  . .
Wir betrachten also eine beliebig vorgegebene reelle Zahlen  und und  mit mit 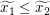 und wollen und wollen 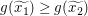 zeigen. zeigen.
Wegen 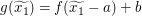 und und 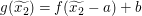 ist also ist also 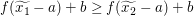 zu zeigen. zu zeigen.
Um eine Beziehung zwischen 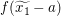 und und 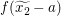 herzustellen, wollen wir die Voraussetzung, dass herzustellen, wollen wir die Voraussetzung, dass 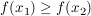 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  gilt, auf gilt, auf 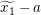 und und 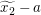 anwenden. Tatsächlich sind beides reelle Zahlen und wegen anwenden. Tatsächlich sind beides reelle Zahlen und wegen 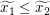 gilt auch gilt auch 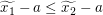 . Also erhalten wir . Also erhalten wir 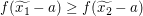 . .
Nun folgt unmittelbar die gewünschte Ungleichung 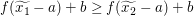 . .
Lösungsvorschlag:
Zu zeigen ist, dass 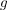 monoton fallend ist, d.h. dass monoton fallend ist, d.h. dass 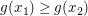 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  gilt. gilt.
Seien also  und und  reelle Zahlen mit reelle Zahlen mit 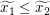 . Zu zeigen ist . Zu zeigen ist 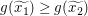 . .
Aus 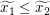 folgt folgt 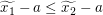 . .
Da 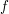 monoton fallend ist, gilt monoton fallend ist, gilt 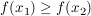 für alle reellen Zahlen für alle reellen Zahlen  und und  mit mit  . .
Insbesondere gilt 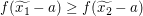 . .
Es folgt 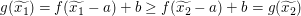 , was zu zeigen war. , was zu zeigen war.
|