Benutzer:tobit09/Beweis-Tutorial A20Beweis-Tutorial
 4. "für alle"-Aussagen 4. "für alle"-Aussagen
Lösungsvorschlag Aufgabe 20
Aufgabe:
Sei  eine Funktion, die sowohl gerade als auch ungerade ist. Zeige eine Funktion, die sowohl gerade als auch ungerade ist. Zeige 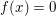 für alle reellen Zahlen für alle reellen Zahlen  . (Tipp: Gemäß Aufgabe 16 gilt: Für alle reellen Zahlen . (Tipp: Gemäß Aufgabe 16 gilt: Für alle reellen Zahlen  mit mit 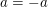 gilt gilt 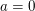 .) .)
Überlegungen zur Lösung:
Gegeben:
Funktion 
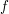 gerade, d.h. gerade, d.h. 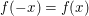 für alle reellen Zahlen für alle reellen Zahlen  . .
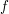 ungerade, d.h. ungerade, d.h. 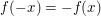 für alle reellen Zahlen für alle reellen Zahlen  . .
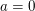 gilt für alle reellen Zahlen gilt für alle reellen Zahlen  mit mit 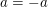 (gemäß Aufgabe 16). (gemäß Aufgabe 16).
Zu zeigen:
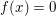 für alle reellen Zahlen für alle reellen Zahlen  . .
Wir betrachten also eine beliebig vorgegebene reelle Zahl 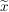 und wollen und wollen 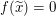 zeigen. zeigen.
Um 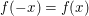 für alle reellen Zahlen für alle reellen Zahlen  und und 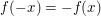 für alle reellen Zahlen für alle reellen Zahlen  gewinnbringend nutzen zu können, werden wir diese beiden Aussagen auf die reelle Zahl gewinnbringend nutzen zu können, werden wir diese beiden Aussagen auf die reelle Zahl 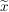 anwenden. anwenden.
Um den Tipp 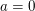 für alle reellen Zahlen für alle reellen Zahlen  mit mit 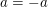 gewinnbringend nutzen zu können, brauchen wir eine reelle Zahl gewinnbringend nutzen zu können, brauchen wir eine reelle Zahl 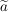 , von der wir , von der wir 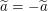 wissen. Da wir wissen. Da wir 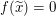 zeigen wollen, wäre ideal, wenn wir zeigen wollen, wäre ideal, wenn wir 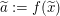 wählen könnten, also wenn es uns gelänge, wählen könnten, also wenn es uns gelänge, 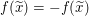 zu zeigen. zu zeigen.
Alles Weitere könnt ihr dem unten stehenden Lösungsvorschlag entnehmen.
Lösungsvorschlag:
Sei 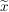 eine reelle Zahl. Zu zeigen ist eine reelle Zahl. Zu zeigen ist 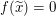 . .
Gegeben ist die Bedingung 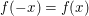 für alle reellen Zahlen für alle reellen Zahlen  . Da . Da 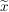 eine reelle Zahl ist, gilt also eine reelle Zahl ist, gilt also 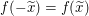 . .
Weiterhin ist die Bedingung 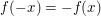 für alle reellen Zahlen für alle reellen Zahlen  gegeben. Da gegeben. Da 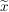 eine reelle Zahl ist, gilt also eine reelle Zahl ist, gilt also 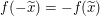 . .
Zusammengenommen erhalten wir 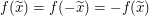 . (*) . (*)
Nach Aufgabe 16 gilt 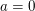 für alle reellen Zahlen für alle reellen Zahlen  mit mit 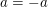 . .
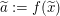 ist gemäß (*) eine reelle Zahl mit ist gemäß (*) eine reelle Zahl mit 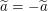 . .
Also 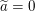 . .
Somit gilt 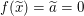 , was zu zeigen war. , was zu zeigen war.
|