DarstellungsmatrixDie Darstellungsmatrix
Beschreibung
Die Darstellungsmatrix 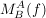 einer linearen Abbildung einer linearen Abbildung 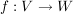 von zwei Vektorräumen V und W mit Basen A von V und B von W ist diejenige Matrix, die einen Vektor aus V, dessen Darstellung v bzgl Basis A gegeben ist, mit f abbildet aber die Darstellung f(v) des Bildvektors bzgl Basis B umwandelt. von zwei Vektorräumen V und W mit Basen A von V und B von W ist diejenige Matrix, die einen Vektor aus V, dessen Darstellung v bzgl Basis A gegeben ist, mit f abbildet aber die Darstellung f(v) des Bildvektors bzgl Basis B umwandelt.
Der wesentliche Zusammenhang zwischen der Abbildung und der Darstellungsmatrix ist : Für jeden Vektor v aus V soll gelten : 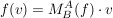
D.H es soll Folgendes gelten:
seien 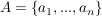 und und 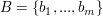 die Basen und seien die Basen und seien 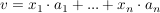 und und 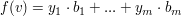 die Basisdarstellungen von v bzgl A bzw. f(v) bzgl B. die Basisdarstellungen von v bzgl A bzw. f(v) bzgl B.
Dann : 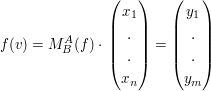
Erläuterung
Jede lineare Abbildung lässt sich durch eine Darstellungsmatrix beschreiben, diese ist eindeutig für fest gewählte Basen.
(Es gilt sogar die Umkehrung : Jede Matrix stellt eine lineare Abbildung dar !)
Es kann von Vorteil sein eine Abbildung einfach durch eine Matrix darzustellen und dann alle Eigenschaften und Berechnungen mit der Matrix zu machen, denn hierfür stehen ein weites Gebiet von Methoden zur Verfügung.
( Eigenwert & Co)
Bestimmung der Darstellungsmatrix
Für den Umgang mit Darstellungsmatrizen ist folgender Satz sehr wichtig:
Die Bilder der Basisvektoren stehen als Spalten in der Darstellungsmatrix.
Begründung : Einen Vektor v kann man bzgl der Basis A wie oben eindeutig darstellen als Linearkombination der Basisvektoren.
Die Linearität der Abbildung bewirkt, dass man f(v) direkt aus den Bildern der Basisvektoren ablesen kann:
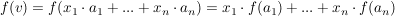
Wenn die Bilder der Basisvektoren 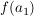 bis bis 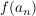 als Elemente in W selbst wieder in Basisdarstellung B gegeben sind, liefert die Definition der Multiplikation einer Matrix mit einem Vektor gerade obiges Ergebnis wenn die Bilder als Elemente in W selbst wieder in Basisdarstellung B gegeben sind, liefert die Definition der Multiplikation einer Matrix mit einem Vektor gerade obiges Ergebnis wenn die Bilder 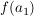 bis bis 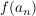 als Spalten in der Matrix als Spalten in der Matrix 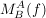 stehen. stehen.
Besonderheiten
1) Streng genommen müssten auch bei jeder Beschreibung von Abbildungen dabei stehen, welche Basen man dabei betrachtet, wenn dies nicht der Fall ist, kann man normaler Weise davon ausgehen, dass man die kanonische Basen meint (in beiden Vektorräumen).
2) Die oben genannten Vektorräume müssen natürlich nicht verschieden sein , also bei V=W , kann man Endomorphismen (Abbildungen in sich selbst) betrachten, wobei auch A=B sein kann, dann schreibt man auch oft die verkürzende Schreibweise : 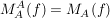
(und A kann man auch noch weglassen, wenn es klar (oder unwichtig) ist, um welche Basis es sich handelt...)
3) Die Darstellungsmatrix der Identität 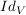 ist bei einer Basis A von V gleich der Einheitsmatrix ist bei einer Basis A von V gleich der Einheitsmatrix 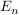 wenn V n-dimensional ist. wenn V n-dimensional ist.
Bei verschiedenen Basen ist sie gerade die Transformationsmatrix eines Basiswechsels.
4) Wenn man die Darstellungsmatrix 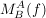 kennt bzw. leicht ermitteln kann (bei Standardbasen beispielsweise) , dann kann man die Darstellungsmatrix kennt bzw. leicht ermitteln kann (bei Standardbasen beispielsweise) , dann kann man die Darstellungsmatrix 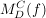 bzgl zweier anderer Basen mit Hilfe der Transformationsformel berechnen. bzgl zweier anderer Basen mit Hilfe der Transformationsformel berechnen.
Beispiel
gegeben sei die Abbildung 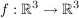 durch: durch:
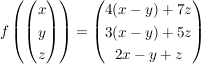
und man möchte die Darstellungsmatrix bzgl Standardbasis bestimmen.
Also nach obigen wichtigen Satz muss man die Bilder der Basisvektoren berechnen:
für den ersten Basisvektor 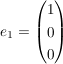 gilt also für x=1 und y=z=0 eingesetzt in obige gegebene Gleichung: gilt also für x=1 und y=z=0 eingesetzt in obige gegebene Gleichung:
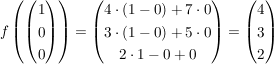
Dies ist dann die erste Spalte. Wenn man dies auch mit den beiden anderen Basisvektoren 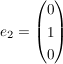 und und 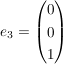 macht, erhält man : macht, erhält man : 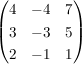 als Darstellungsmatrix bzgl Standardbasis. als Darstellungsmatrix bzgl Standardbasis.
Wer dieses Beispiel auch noch mit einer anderen Basis sehen möchte, kann sich das Beispiel bei der Transformationsformel ansehen.
Oder alternativ in ![Link auf "https://matheraum.de/read?t=69283" [link]](/images/popup.gif) DIESEN Artikel (Matheraum) DIESEN Artikel (Matheraum)
Matheraum Links
![Link auf "https://matheraum.de/read?t=2092" [link]](/images/popup.gif) ein weiteres Beispiel (Matheraum) ein weiteres Beispiel (Matheraum)
![Link auf "http://matheplanet.com/matheplanet/nuke/html/article.php?sid=368" [link]](/images/popup.gif) guter Artikel (MathePlanet) guter Artikel (MathePlanet)
![Link auf "http://de.wikipedia.org/wiki/Darstellungsmatrix#Darstellungsmatrix" [link]](/images/popup.gif) entspr. Artikel auf Wikipedia entspr. Artikel auf Wikipedia
|