KoordinatenformBegriff Koordinatenform
Ebenengleichung:
mit a, b, c, d beliebige reelle Zahlen.
Kann man die Parameter einer Ebenengleichung in Parameterform eliminieren, so dass lediglich die Koordinaten eines beliebigen Punktes der Ebene in der Gleichung auftreten,
so nennt man diese auch Ebenengleichung in Koordinatenform oder parameterfreie Form der Ebenengleichung.
Von der Koordinatenform zur Parameterform:
man löst zunächst die Koordinatengleichung nach einer Koordinate auf und ersetzt die beiden anderen durch die Parameter r und s.
Beispiel
Aus 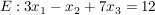 folgt: folgt:
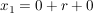
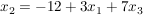
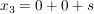
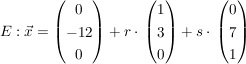
|