ParameterformBegriff Parameterform
Da die folgenden Gleichungen die Parameter r und s enthalten, nennt man diese auch
Gleichungen in Parameterform
Geradengleichung in Parameterform.
- Jede Gerade lässt sich durch eine Gleichung folgender Form beschreiben.
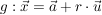
Hierbei ist 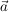 ein Stützvektor (Aufhängepunkt), ein Stützvektor (Aufhängepunkt), 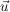 ein Richtungsvektor und r eine reelle Zahl (Parameter). ein Richtungsvektor und r eine reelle Zahl (Parameter).
Ebenengleichung in Parameterform
- Jede Ebene läßt sich darstellen durch eine Gleichung folgender Form:
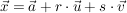
Hierbei ist 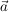 ein Stützvektor (Aufhängepunkt), ein Stützvektor (Aufhängepunkt), 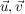 sind zwei linear unabhängige Richtungsvektoren und r,s zwei reelle Zahlen (Parameter). sind zwei linear unabhängige Richtungsvektoren und r,s zwei reelle Zahlen (Parameter).
Koordinatenform
- Jede Parametergleichung läßt sich durch Eliminieren der Parameter in die Koordinatenform umwandeln.
umwandeln in ein Gleichungssystem, bei dem man die Parameter r und s durch  , ,  und und 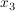 berechnet: berechnet:
als Lösung die parameterfreie Form der Ebene.
|