LängeDefinition Länge
- Länge eines Vektors
- Länge eines Intervalls
- (Bogen-) Länge einer Funktionskurve
- Länge einer Kurve (allgemein)
-=Schule=-
Definition Länge eines Vektors
Unter dem Betrag eines Vektors 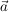 versteht man die Länge der zu versteht man die Länge der zu 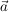 gehörenden Pfeile. gehörenden Pfeile.
Der Betrag wird mit 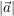 bezeichnet. bezeichnet.
Kennt man die Komponenten des Vektors 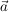 in einem kartesischen Koordinatensystem, so kann man seinen Betrag mithilfe des Satzes des Pythagoras berechnen: in einem kartesischen Koordinatensystem, so kann man seinen Betrag mithilfe des Satzes des Pythagoras berechnen:
Definition Länge eines Intervalls
Die Länge eines Intervalls ![$ [a,b] $ $ [a,b] $](/teximg/9/5/00000959.png) berechnet man durch: |b - a| . berechnet man durch: |b - a| .
Definition (Bogen-) Länge einer Funktionskurve
Sei ![$ f: [a,b]\to\IR $ $ f: [a,b]\to\IR $](/teximg/2/0/00167602.png) eine differenzierbare Funktion, und eine differenzierbare Funktion, und ![$ G_f=\{(x,f(x))\ |\ x\in [a,b]\} $ $ G_f=\{(x,f(x))\ |\ x\in [a,b]\} $](/teximg/9/7/00388079.png) ihr Graph. ihr Graph.
Dann heißt
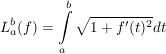
die Länge des Graphen von f über dem Intervall ![$ [a,b] $ $ [a,b] $](/teximg/9/5/00000959.png) . .
Universität
Definition Länge einer Kurve
Sei ![$ f:[a,b]\to V $ $ f:[a,b]\to V $](/teximg/1/8/00388081.png) eine Kurve in V. eine Kurve in V.
Dann heißt das Supremum über die Längen aller Streckenzüge ![$ [f(t_0),\ldots,f(t_m)] $ $ [f(t_0),\ldots,f(t_m)] $](/teximg/2/8/00388082.png) , wobei , wobei 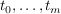 alle endlichen Folgen alle endlichen Folgen 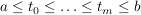 durchläuft, die Länge durchläuft, die Länge
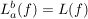
von f.
Ist 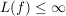 , so heißt f rektifizierbar. , so heißt f rektifizierbar.
Quelle: (1)
Wichtige Sätze
Quelle: (1)
Quelle: (1) isbn3411141816
|