NullstelleNullstelle
... heißt diejenige Stelle auf der x-Achse, an der der Graph der Funktion die x-Achse schneidet oder berührt.
Das bedeutet, dass dort die Funktion den Wert 0 hat:
Sei als Beispiel 
dann gilt: f(3) = 0 und f(-4) = 0
 oder oder  sind also die Nullstellen dieser Funktion. sind also die Nullstellen dieser Funktion.
Allgemein:
man findet alle Nullstellen einer Funktion f(x),
indem man die Gleichung f(x)=0 löst.
Bemerkungen:
1. Habe eine ganzrationale Funktion f an der Stelle 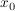 eine Nullstelle mit der Vielfachheit n. eine Nullstelle mit der Vielfachheit n.
- Ist n ungerade, dann schneidet der Graph von f die x-Achse.
(Man sagt, die Funktion hat an der Stelle 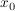 eine Nullstelle mit Vorzeichenwechsel eine Nullstelle mit Vorzeichenwechsel
oder auch: "die Funktion hat dort eine Durchgangsstelle").
- Ist n gerade, dann berührt der Graph von f die x-Achse.
(Man sagt, die Funktion hat an der Stelle 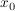 eine Nullstelle ohne Vorzeichenwechsel eine Nullstelle ohne Vorzeichenwechsel
oder auch: "die Funktion hat dort eine Berührstelle").
2. Ist  eine Nullstelle einer ganzrationalen Funktion f, dann kann man f(x) schreiben als: eine Nullstelle einer ganzrationalen Funktion f, dann kann man f(x) schreiben als:
mit einer ganzrationalen Funktion g, deren Grad um 1 niedriger ist als der Grad der Funktion f.
Damit kann man den Grad einer Funktion schrittweise erniedrigen, bis man endlich eine Funktion 2. Grades erhält, die man mit der p/q-Formel oder der ABC-Formel lösen kann.
3. Hat eine Funktion die Nullstellen  und und 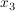 , so gilt: , so gilt:
Das absolute Glied enthält also stets die Nullstellen als Faktoren.
Bei ganz-rationalen Funktionen (in der Schule) lohnt sich die Fahndung nach "kleinen" ganzen Zahlen:  . .
|