Quadratwurzel einer reellen ZahlDefinition Quadratwurzel einer reellen Zahl
Die Quadratwurzel einer nichtnegativen reellen Zahl  (im Zeichen (im Zeichen  ) ist definiert als diejenige nichtnegative reelle Zahl ) ist definiert als diejenige nichtnegative reelle Zahl 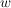 (also (also 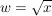 ), so dass ), so dass 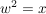 gilt. gilt.
In mathematischen Symbolen:
Für jedes 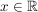 , , 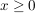 ist ist 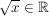 jene Zahl mit den folgenden zwei Eigenschaften: jene Zahl mit den folgenden zwei Eigenschaften:
1.) 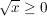
2.) 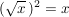 . .
Die Zahl (oder den Term) unter dem Wurzelzeichen nennt man Radikand.
Beispiele.
1.) Es gilt 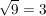 , nicht aber , nicht aber 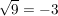 . .
Mit anderen Worten:
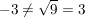 . .
2.) Es gilt 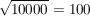 . .
3.) 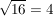 . .
Bemerkungen.
Quadratwurzel ohne TR: Quadratwurzelbestimmung
1.) In einem Quadrat der Seitenlänge 1 cm hat die Diagonale die Länge 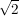 cm (nach Pythagoras). cm (nach Pythagoras).
2.) Wir führen den Beweis, dass 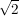 keine rationale Zahl ist. keine rationale Zahl ist.
Beweis:
Angenommen, 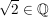 . Dann existieren . Dann existieren 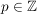 , , 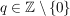 , so dass gilt: , so dass gilt:
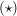 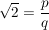 . .
O.B.d.A. können wir den Bruch 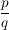 als vollständig gekürzt annehmen. als vollständig gekürzt annehmen.
Aus der Gleichung 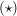 folgt: folgt:
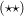 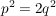 . .
Die letzte Gleichung impliziert, dass 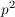 und damit auch und damit auch 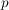 gerade sein muss (beachte dabei: gerade sein muss (beachte dabei: 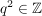 ). ).
(Denn: Ist 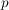 ungerade, also ungerade, also 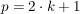 (mit einem festen (mit einem festen 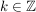 ), so gilt: ), so gilt:
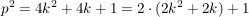 und wegen und wegen 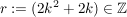 ist ist 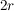 gerade, also gerade, also 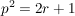 ungerade! Folglich kann, wenn ungerade! Folglich kann, wenn 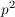 gerade ist, auch gerade ist, auch 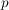 nur gerade sein!) nur gerade sein!)
Weil wir nun (o.B.d.A.) den Bruch 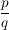 als vollständig gekürzt angenommen haben, folgt deswegen, dass als vollständig gekürzt angenommen haben, folgt deswegen, dass 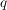 ungerade sein muss. (Denn wären ungerade sein muss. (Denn wären 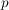 und und 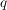 beide gerade, so hätten sie ja den gemeinsamen Teiler beide gerade, so hätten sie ja den gemeinsamen Teiler 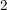 , und damit wäre der Bruch , und damit wäre der Bruch 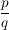 nicht vollständig gekürzt.) nicht vollständig gekürzt.)
Falls also 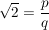 (mit (mit 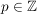 und und 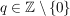 ) gilt, so müssen demnach ) gilt, so müssen demnach 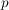 gerade und gerade und 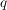 ungerade sein. Es existieren also ungerade sein. Es existieren also 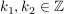 , so dass: , so dass:
(I) 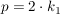 und und
(II) 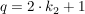 gelten. gelten.
Setzen wir (I) und (II) in 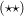 ein, so folgt: ein, so folgt:
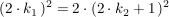
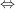
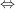
 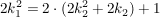
Nun ist aber 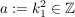 und deswegen ist und deswegen ist 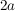 eine gerade Zahl. Andererseits ist eine gerade Zahl. Andererseits ist 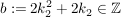 und deswegen ist und deswegen ist 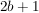 eine ungerade Zahl. Mit diesen Definition von eine ungerade Zahl. Mit diesen Definition von  bzw. bzw. 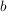 gilt aber: gilt aber:
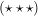 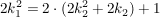
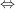
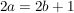 . .
Die letzte Gleichung würde aber bedeuten, dass eine gerade Zahl mit einer ungeraden Zahl übereinstimmen würde. Das ist offenbar ein Widerspruch und der Beweis, dass 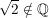 gilt, ist hier zu Ende. gilt, ist hier zu Ende. 
3.) Man beachte, dass i.A. die Gleichungen
(1.) 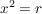 und und
(2.) __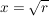 (für ein festes
(für ein festes 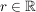 , , 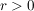 ) nicht äquivalent sind.
Für z.B. ) nicht äquivalent sind.
Für z.B. 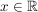 gilt stets, dass aus __(2.) die Gleichung (1.) folgt. Jedoch folgt aus der Gleichung (1.) nicht stets die Gleichung (2.), denn die Gleichung (1.) besitzt auch die Lösung gilt stets, dass aus __(2.) die Gleichung (1.) folgt. Jedoch folgt aus der Gleichung (1.) nicht stets die Gleichung (2.), denn die Gleichung (1.) besitzt auch die Lösung 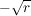 , welche in (2.) nicht enthalten ist. , welche in (2.) nicht enthalten ist.
Es gelten aber, für (z.B.) 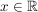 , folgende äquivalente Umformungen der Gleichung (1.): , folgende äquivalente Umformungen der Gleichung (1.):
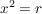 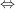 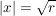 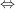 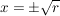
(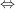 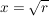 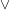 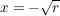 ). ).
|