QuaternionengruppeDefinition Quaternionengruppe
Universität
Es sei
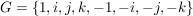
mit neutralem Element 1.
Man rechnet mit den Vorzeichen, wie man es gewöhnt ist, zum Beispiel
(-1)(-1) =1,
(-1)i = -i,
(-i)(-j) = ij,
etc.
Ferner sei
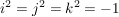 , ,
ij=k,
jk=i,
ki=j.
Durch diese Angaben ist die Strukturtafel vollständig bestimmt.
Man kann diese Gruppe als die Gruppe der invertierbaren Elemente der multiplikativen Halbgruppe der Quaternionen mit Koeffizienten aus 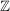 ansehen. ansehen.
Daher heißt diese Gruppe auch Quaternionengruppe.
Quelle: isbn3446130799
|