UntergruppeDefinition Untergruppe
Universität
Eine nichtleere Teilmenge 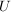 einer Gruppe einer Gruppe  heißt eine Untergruppe von heißt eine Untergruppe von  , wenn , wenn 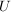 mit der Verknüpfung aus mit der Verknüpfung aus  selbst eine Gruppe ist. selbst eine Gruppe ist.
Setzt man für zwei nichtleere Teilmenge 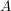 und und 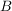 einer Gruppe einer Gruppe 
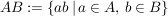
und
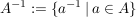 , ,
so kann man die folgenden Unterraumkriterien formulieren:
Es sei  eine Gruppe und eine Gruppe und 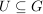 eine nichtleere Teilmenge. Dann sind die folgenden Aussagen äquivalent: eine nichtleere Teilmenge. Dann sind die folgenden Aussagen äquivalent:
a) 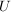 ist eine Untergruppe von ist eine Untergruppe von 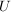 . .
b) Aus 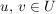 folgt folgt 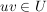 und und 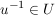 . .
c) 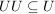 und und 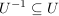 . .
d) 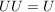 und und 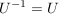 . .
e) Aus 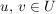 folgt: folgt: 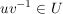 . .
f) 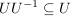 . .
g) 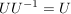 . .
Für endliche Gruppen kann man noch ein günstigeres Kriterium formulieren:
Eine nichtleere endliche Teilmenge 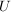 einer Gruppe einer Gruppe  ist genau dann eine Untergruppe, wenn mit alle ist genau dann eine Untergruppe, wenn mit alle 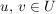 auch auch 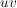 in in 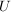 liegt, d.h. wenn liegt, d.h. wenn 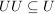 gilt. gilt.
Beispiele
a) In jeder Gruppe  sind stets sind stets 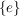 und und  Untergruppen, die sogenannten trivialen Untergruppen. Klar ist auch, dass jede Untergruppe Untergruppen, die sogenannten trivialen Untergruppen. Klar ist auch, dass jede Untergruppe 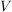 einer Untergruppe einer Untergruppe 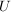 von von  auch Untegrgruppe von auch Untegrgruppe von  ist. ist.
b) 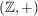 ist eine Untergruppe von ist eine Untergruppe von 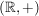 , , 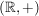 ist eine Untergruppe von ist eine Untergruppe von 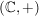 . Für jede natürliche Zahl . Für jede natürliche Zahl  ist ist 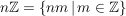 eine Untergruppe von eine Untergruppe von 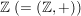 . Ist . Ist 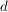 ein Teiler von ein Teiler von  , dann ist jedes Vielfache von , dann ist jedes Vielfache von  auch Vielfaches von auch Vielfaches von 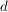 . Folglich ist . Folglich ist 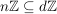 , und es ist , und es ist 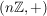 eine Untergruppe von eine Untergruppe von 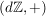 . .
c) Sei 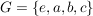 die Kleinsche Vierergruppe. Es sind die Kleinsche Vierergruppe. Es sind 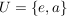 , , 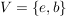 und und 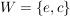 Untergruppen von Untergruppen von  . .
d) Sei 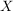 eine nichtleere Menge, eine nichtleere Menge, 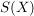 die symmetrische Gruppe von die symmetrische Gruppe von 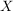 und für ein festes Element und für ein festes Element 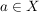 sei sei
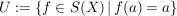 . .
Für 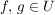 gilt: gilt: 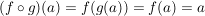 ; d.h. ; d.h. 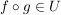 . Außerdem ist . Außerdem ist 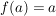 äquivalent zu äquivalent zu 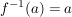 , also ist auch , also ist auch 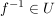 . Daher ist . Daher ist 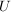 eine Untergruppe von eine Untergruppe von 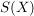 . .
e) In der symmetrischen Gruppe 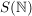 betrachten wir für jedes betrachten wir für jedes 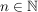 die Teilmenge die Teilmenge
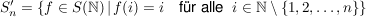 . .
Die 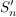 sind Untergruppen von sind Untergruppen von 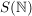 , Außerdem sieht man, dass für , Außerdem sieht man, dass für 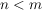 auch auch 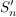 eine Untergruppe von eine Untergruppe von 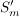 ist. Es handelt sich bei diesen ist. Es handelt sich bei diesen 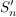 nur um eine andere Schreibweise der symmetrischen Gruppen nur um eine andere Schreibweise der symmetrischen Gruppen 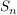 (triviale Isomorphie). Fasst man die (triviale Isomorphie). Fasst man die 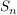 in der angegebenen Weise als Untergruppen von in der angegebenen Weise als Untergruppen von 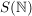 auf, so ist für auf, so ist für 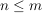 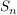 eine Untergruppe von eine Untergruppe von 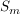 . .
f) Wie man durch einfaches Ausrechnen der Produkte bestätigt, ist
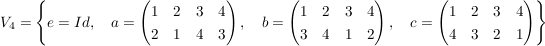
eine Untergruppe von 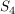 . Dies ist eine Realisierung der Kleinschen Vierergruppe, da durch die Festlegung . Dies ist eine Realisierung der Kleinschen Vierergruppe, da durch die Festlegung 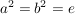 die Struktur der Vierergruppe bereits festgelegt ist. die Struktur der Vierergruppe bereits festgelegt ist.
g) Der Satz von Cayley lautet unter Verwendung des Begriffs Untergruppe: Jede Gruppe  ist isomorph zu einer Untergruppe der symmetrischen Gruppe ist isomorph zu einer Untergruppe der symmetrischen Gruppe 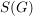 . .
Interessant ist es natürlich, wie sich Untergruppen bei homomorphen Abbildungen verhalten:
Es seien 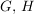 Gruppen, Gruppen, 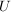 eine Untergruppe von eine Untergruppe von  , , 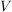 eine Untergruppe von eine Untergruppe von 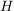 und und 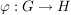 ein Homomorphismus. Dann gilt: ein Homomorphismus. Dann gilt:
a) Das Bild 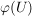 ist eine Untergruppe von ist eine Untergruppe von 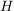 . .
b) Das Urbild 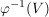 ist eine Untergruppe von ist eine Untergruppe von  . .
Die Sonderfälle 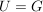 und und 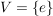 ergeben: ergeben:
a) 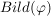 ist eine Untergruppe von ist eine Untergruppe von 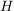 . .
b) 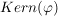 ist eine Untergruppe von ist eine Untergruppe von  . .
Als Bild eines inneren Automorphismismus ist mit jeder Untergruppe 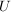 von von  und jedem und jedem 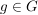 auch auch 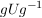 eine Untergruppe von eine Untergruppe von  . Die Untergruppen . Die Untergruppen 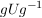 , , 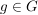 , heißen die zu , heißen die zu 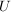 konjugierten Untergruppen. Untergruppen konjugierten Untergruppen. Untergruppen 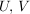 von von  heißen also konjugiert, wenn es ein heißen also konjugiert, wenn es ein 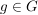 gibt mit gibt mit 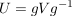 . Man sieht leicht ein, dass die durch " . Man sieht leicht ein, dass die durch "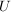 ist konjugiert zu ist konjugiert zu 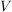 " definierte Relation auf der Menge der Untergruppen von " definierte Relation auf der Menge der Untergruppen von  eine Äquivalenzrelation ist. Die zugehörigen Äquivalenzklassen heißen Klassen konjugierter Untergruppen. Die Menge alles Untergruppen zerfällt also in disjunkte Klassen konjugierter Untergruppen. In abelschen Gruppen gilt stets eine Äquivalenzrelation ist. Die zugehörigen Äquivalenzklassen heißen Klassen konjugierter Untergruppen. Die Menge alles Untergruppen zerfällt also in disjunkte Klassen konjugierter Untergruppen. In abelschen Gruppen gilt stets 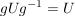 , d.h. in abelschen Gruppen bestehen die Klassen konjugierter Untergruppen jeweils aus genau einem Element. , d.h. in abelschen Gruppen bestehen die Klassen konjugierter Untergruppen jeweils aus genau einem Element.
Wie verhalten sich Untergruppen bei Mengenoperationen?
1) inneres Produkt
Es seien 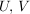 Untergruppen einer Gruppe Untergruppen einer Gruppe  . Es ist . Es ist 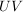 genau dann eine Untergruppe, wenn genau dann eine Untergruppe, wenn 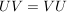 gilt. Sind also gilt. Sind also 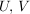 Untergruppen einer abelschen Gruppe Untergruppen einer abelschen Gruppe  , dann ist , dann ist 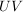 eine Untergruppe von eine Untergruppe von  . .
2) Durchschnitt
Ist  eine Gruppe, eine Gruppe, 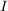 eine nichtleere Menge und eine nichtleere Menge und 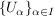 eine Familie von Untergruppen von eine Familie von Untergruppen von  , dann ist auch , dann ist auch 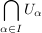 eine Untergruppe von eine Untergruppe von  . .
3) Vereinigung
Die Vereinigung von Untergruppen ist im allgemeinen keine Untergruppe.
Quelle: isbn3446130799
|