orthogonalDefinition orthogonal
Schule
- orthogonale Gerade
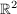 : Schneiden sich zwei Geraden im : Schneiden sich zwei Geraden im 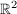 mit einen rechten Winkel (= 90°), mit einen rechten Winkel (= 90°), 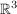 : Gilt für die Richtungsvektoren : Gilt für die Richtungsvektoren 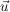 und und 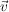 zweier Geraden im zweier Geraden im 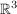 : :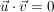 , ,
- so sind sie orthogonal zueinander.
Zwei Geraden im 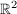 sind genau dann orthogonal, wenn für ihre Steigungen gilt: sind genau dann orthogonal, wenn für ihre Steigungen gilt: 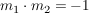 . .
Zwei Geraden im 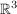 sind genau dann orthogonal, wenn das Skalarprodukt ihrer Richtungsvektoren Null ergibt. sind genau dann orthogonal, wenn das Skalarprodukt ihrer Richtungsvektoren Null ergibt.
- orthogonaler Vektor
Für orthogonale Vektoren gilt sinngemäß dasselbe:
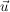 orthogonal zu orthogonal zu 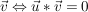
Universität
|