Zahlenmenge(Weitergeleitet von reell) 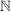 : die Menge der natürlichen Zahlen : die Menge der natürlichen Zahlen
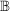 : die Menge der Bruchzahlen : die Menge der Bruchzahlen
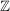 : die Menge der ganzen Zahlen : die Menge der ganzen Zahlen
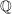 : die Menge der rationalen Zahlen : die Menge der rationalen Zahlen
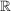 : die Menge der reellen Zahlen : die Menge der reellen Zahlen
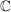 : die Menge der komplexen Zahlen : die Menge der komplexen Zahlen
Es gilt: 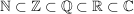
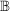 ist die Menge der positiven rationalen Zahlen: ist die Menge der positiven rationalen Zahlen: 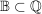
In diesen Zahlenmengen sind zwei Verknüpfungen definiert:
"+" : die Addition und ihre Umkehrung, die Subtraktion "-"
" " : die Multiplikation und ihre Umkehrung, die Division ":". " : die Multiplikation und ihre Umkehrung, die Division ":".
natürliche Zahlen
Die natürlichen Zahlen bilden die Menge
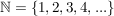
Es sind also die Zahlen, mit denen man zählen kann.
Nimmt man die 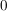 dazu, so erhält man dazu, so erhält man
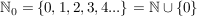
Viele Autoren behandeln die Null direkt als natürliche Zahl und verstehen under 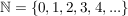 . Im Zweifel sollte die genaue Definition im jeweiligen Buch nachgeschlagen werden. . Im Zweifel sollte die genaue Definition im jeweiligen Buch nachgeschlagen werden.
ganze Zahlen
Ein Element der Menge 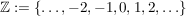 heißt ganze Zahl. heißt ganze Zahl.
Jede ganze Zahl ist auch eine rationale Zahl, reelle Zahl.
Die Menge der natürlichen Zahlen ist eine Teilmenge der Menge der ganzen Zahlen.
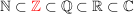
Bruchzahlen
sind Quotienten aus zwei natürlichen Zahlen 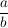 , bei dem , bei dem 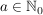 und und 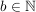 gilt. gilt.
 nennt man den Zähler des Bruches und nennt man den Zähler des Bruches und 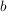 den Nenner. den Nenner.
rationale Zahlen und Dezimalzahlen
Die Menge der rationalen Zahlen ist die Vereinigung der Menge der Bruchzahlen mit der Menge der (negativen) Gegenzahlen der Bruchzahlen.
Die rationalen Zahlen können auf dem Zahlenstrahl angeordnet werden und liegen dort dicht.
Das bedeutet, dass zwischen je zwei "benachbarten" Brüchen stets mind. ein weiterer Bruchzahl angegeben werden kann:
Zu den rationalen Zahlen gehören auch die Dezimalzahlen, also diejenigen Brüche, die im Nenner eine Zehnerpotenz enthalten
(= endliche Dezimalbrüche),
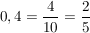 oder 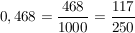
und
die periodischen Dezimalbrüche:
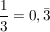 oder 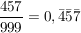
irrationale Zahlen
Die Menge der irrationalen Zahlen umfasst alle unendlichen, nichtperiodischen Dezimalbrüche.
Beispiele für irrationale Zahlen:
reelle Zahlen
Die Menge 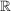 der reellen Zahlen der reellen Zahlen
umfasst alle endlichen und periodischen Dezimalbrüche und die unendlichen Dezimalbrüche.
Sie ist die Vereinigung der Menge 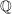 der rationalen Zahlen mit der Menge der rationalen Zahlen mit der Menge 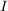 der irrationalen Zahlen, wobei die irrationalen Zahlen unendliche, nichtperiodische Dezimalbrüche sind. der irrationalen Zahlen, wobei die irrationalen Zahlen unendliche, nichtperiodische Dezimalbrüche sind.
Beispiele für irrationale Zahlen:
komplexe Zahlen
Komplexe Zahlen sind Zahlen, die in der Form a+bi dargestellt werden, wobei i für die imaginäre Einheit steht.
Es gilt 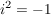 , wodurch auch Gleichungen der Form , wodurch auch Gleichungen der Form 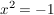 gelöst werden können. gelöst werden können.
siehe auch: ![Link auf "http://www.mathe-online.at/mathint/zahlen/i.html#Zahlenmengen" [link]](/images/popup.gif) Zahlenmengen in mathe-online.at Zahlenmengen in mathe-online.at
|