PotenzmengeDefinition Potenzmenge
Schule
Sei M eine Menge.
Die Menge 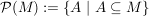 heißt Potenzmenge.
Eigenschaften der Potenzmenge
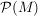 ist also eine Menge, die aus allen Teilmengen von M besteht. ist also eine Menge, die aus allen Teilmengen von M besteht.
Es gilt: 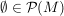 und und 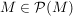 , da , da 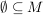 und und 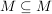 . In Worten: Die leere Menge und die Menge M selbst ist in der Potenzmenge von M enthalten. . In Worten: Die leere Menge und die Menge M selbst ist in der Potenzmenge von M enthalten.
Satz: Für endliche Mengen M mit |M|=n gilt: 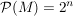 .
Beweis. (durch vollständige Induktion)
Teilmengen der Potenzmenge heißen Mengensysteme.
Universität
|