PrämaßDefinition Prämaß
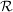 Ring in Ring in 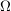 , , ![$ \mu:\ \mathcal{R}\to[0,+\infty] $ $ \mu:\ \mathcal{R}\to[0,+\infty] $](/teximg/8/5/00932458.png) Funktion. Funktion.
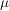 heißt Prämaß (auf heißt Prämaß (auf 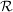 ) wenn ) wenn
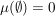 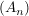 Folge paarweise fremder Mengen Folge paarweise fremder Mengen 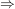 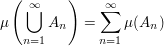 ( ( -Additivität) -Additivität)
Siehe auch: Inhalt, Maß
Beispiele:
1. 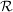 Ring in Ring in 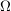 , , 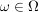 . .
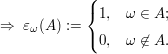 ist ein Prämaß auf ist ein Prämaß auf 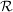 . Es heißt das durch die Einheitsmasse in . Es heißt das durch die Einheitsmasse in 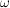 definierte Prämaß auf definierte Prämaß auf 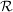
2. 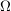 nichtabzählbar (z.B. nichtabzählbar (z.B.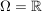 ), ), 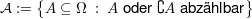 $\sigma$-Algebra. $\sigma$-Algebra. 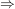 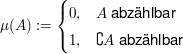 ist Prämaß auf ist Prämaß auf 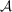 (es ist sogar ein Maß) (es ist sogar ein Maß)
3. 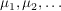 Folge von Inhalten (bzw. Prämaßen) auf Ring Folge von Inhalten (bzw. Prämaßen) auf Ring 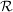 , , 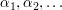 Folge nicht-negativer Zahlen. Folge nicht-negativer Zahlen. 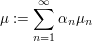 ist Inhalt (bzw. Prämaß) auf ist Inhalt (bzw. Prämaß) auf 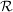
4. Lebesguesches Prämaß
Literatur: isbn3110136252
|